HeldGroupHe

HeldGroupHe[]

represents the sporadic simple Held group .

Details

  • By default, HeldGroupHe[] is represented as a permutation group acting on points {1,…,2058}.

Background & Context

  • HeldGroupHe[] represents the Held group 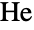, which is a group of order TemplateBox[{2, 10}, Superscript].TemplateBox[{3, 3}, Superscript].TemplateBox[{5, 2}, Superscript].TemplateBox[{7, 3}, Superscript].17. It is one of the 26 sporadic simple groups of finite order. The default representation of HeldGroupHe is as a permutation group on the symbols 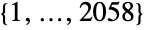having two generators.
  • The Held group 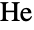is the eleventh smallest of the sporadic finite simple groups. It was discovered by mathematician Dieter Held in the late 1960s. 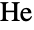is one of a small number of groups that may contain an involution whose centralizer is isomorphic to that of an involution in the Mathieu group 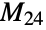. Moreover, 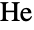centralizes an element of order seven in the monster group. In addition to its many permutation representations, HeldGroupHe can be defined in terms of generators and relations as 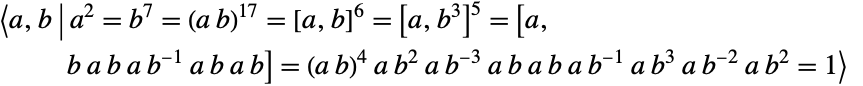, where 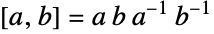. Along with the other sporadic simple groups, played a foundational role in the monumental (and complete) classification of finite simple groups.
  • The usual group theoretic functions may be applied to HeldGroupHe[], including GroupOrder, GroupGenerators, GroupElements and so on. However, due its large order, a number of such group theoretic functions may return unevaluated when applied to it. A number of precomputed properties of the Held group are available via FiniteGroupData["Held","prop"].
  • HeldGroupHe is related to a number of other symbols. HeldGroupHe is one of the eight groups (along with FischerGroupFi22, FischerGroupFi23, FischerGroupFi24Prime, HaradaNortonGroupHN, ThompsonGroupTh, BabyMonsterGroupB and MonsterGroupM) collectively referred to as the "third generation" of sporadic finite simple groups. It is also one of 20 so-called "happy" sporadic groups, which all appear as a subquotient of the monster group.

Examples

Basic Examples  (3)

Order of the Held group:

Number of points moved by the generators of a permutation representation of :

Order of a pseudorandom element of the Held group:

Wolfram Research (2010), HeldGroupHe, Wolfram Language function, https://reference.wolfram.com/language/ref/HeldGroupHe.html.

Text

Wolfram Research (2010), HeldGroupHe, Wolfram Language function, https://reference.wolfram.com/language/ref/HeldGroupHe.html.

CMS

Wolfram Language. 2010. "HeldGroupHe." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/HeldGroupHe.html.

APA

Wolfram Language. (2010). HeldGroupHe. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HeldGroupHe.html

BibTeX

@misc{reference.wolfram_2024_heldgrouphe, author="Wolfram Research", title="{HeldGroupHe}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/HeldGroupHe.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_heldgrouphe, organization={Wolfram Research}, title={HeldGroupHe}, year={2010}, url={https://reference.wolfram.com/language/ref/HeldGroupHe.html}, note=[Accessed: 21-November-2024 ]}