FitRegularization
Details

- Fit and FindFit typically find parameters pars that minimize the norm(res) where res is the residual vector defined as the difference between the model and data response at the data coordinate points. With FitRegularization->rfun, the objective to minimize is norm(residuals)+rfun(pars)
- Fit and FindFit find parameters
 that minimize the norm
that minimize the norm 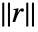 where
where 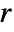 is the residual vector with components given by
is the residual vector with components given by 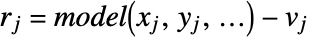 where
where 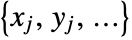 are the data coordinates and
are the data coordinates and 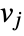 are the data values and model also depends on the parameters.
are the data values and model also depends on the parameters. - Possible settings include:
-
None no regularization rfun regularize with rfun[a] {"Tikhonov", λ} regularize with 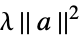
{"LASSO",λ} regularize with 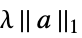
{"Variation",λ} regularize with ![lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a]||^2 lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a]||^2](Files/FitRegularization.en/9.png)
{"TotalVariation",λ} regularize with ![lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a]||_1 lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a]||_1](Files/FitRegularization.en/10.png)
{"Curvature",λ} regularize with ![lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a,2]||^2 lambda||TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a,2]||^2](Files/FitRegularization.en/11.png)
{r1,r2,…} regularize with the sum of terms from r1,…
Examples
open all close allBasic Examples (2)
Applications (5)
Use regularization to stabilize the numerical solution ![]() to
to ![]() where
where ![]() is perturbed:
is perturbed:
The solution found by LinearSolve has very large entries:

Regularized solutions stay much closer to the solution of the unperturbed problem:
Use variation regularization to find a smooth approximation for an input signal:
The output target is a step function:
The input is determined from the output via convolution with ![]() :
:
Without regularization, the predicated response matches the signal very closely, but the computed input has a lot of oscillation:
With regularization of the variation, a much smoother approximation can be found:
Regularization of the input size may also be included:
Smooth a corrupted signal using variation regularization:
Plot the tradeoff between the norm of the residuals and the norm of the variation:
Choose a value of ![]() near where the curve bends sharply:
near where the curve bends sharply:
Use total variation regularization to smooth a corrupted signal with jumps:
Regularize with the parameter ![]() :
:
A smaller value of ![]() gives less smoothing, but the residual norm is smaller:
gives less smoothing, but the residual norm is smaller:
Use LASSO (L1) regularization to find a sparse fit (basis pursuit):
The goal is to approximate the signal with just of few of the thousands of Gabor basis functions:
With ![]() , a fit is found using only 41 of the basis elements:
, a fit is found using only 41 of the basis elements:
Once the important elements of the basis have been found, error can be reduced by finding the least-squares fit to these elements:
With a smaller value ![]() , a fit is found using more of the basis elements:
, a fit is found using more of the basis elements:
History
Text
Wolfram Research (2019), FitRegularization, Wolfram Language function, https://reference.wolfram.com/language/ref/FitRegularization.html.
CMS
Wolfram Language. 2019. "FitRegularization." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FitRegularization.html.
APA
Wolfram Language. (2019). FitRegularization. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FitRegularization.html
BibTeX
@misc{reference.wolfram_2025_fitregularization, author="Wolfram Research", title="{FitRegularization}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/FitRegularization.html}", note=[Accessed: 28-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_fitregularization, organization={Wolfram Research}, title={FitRegularization}, year={2019}, url={https://reference.wolfram.com/language/ref/FitRegularization.html}, note=[Accessed: 28-February-2026]}

