WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

FitRegularization

FitRegularization

FitおよびFindFitのオプションで，モデルのフィットの正則化を指定する．

詳細

FitおよびFindFitは，一般に，norm(res)を最小化するパラメータ pars を求める．res はデータの座標点におけるモデルと応答データの差として定義された残差ベクトルである．FitRegularization->rfun のとき，最小化する目的は norm(residuals)+rfun(pars)である．
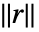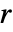FitおよびFindFitは，ノルムを最小化するパラメータを求める．は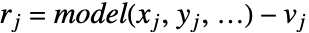で与えられる成分の残差ベクトルである．ここで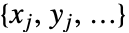，はデータ座標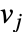，はデータ値で，model はパラメータに依存する．
以下は，使用可能な設定である．

	None	正則化は行わない
	rfun	rfun[a]で正則化
	{"Tikhonov", λ}	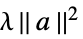で正則化
	{"LASSO",λ}	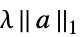で正則化
	{"Variation",λ}	$lambda\|\|TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a]\|\|^2$ で正則化
	{"TotalVariation",λ}	$lambda\|\|TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a]\|\|_1$ で正則化
	{"Curvature",λ}	$lambda\|\|TemplateBox[{Differences, paclet:ref/Differences}, RefLink, BaseStyle -> {2ColumnTableMod}][a,2]\|\|^2$ で正則化
	{r₁,r₂,…}	r₁,…からの項の和で正則化

例題

すべて開くすべて閉じる

例 (2)

チホノフ(Tikhonov)正則化は最適フィットパラメータのサイズを制御する：

正則化しないと，係数が非常に大きくなる：

LASSO正則化は最も効果的な基底要素の選択に使うことができる：

アプリケーション (5)

正則化を使って数値解をに安定させる．ただし，は摂動している：

LinearSolveで求まった解は非常に多くの項を持つ：

正則化された解は非摂動問題の解にはるかに近い：

変動正則化を使って入力信号に対する滑らかな近似を求める：

出力のターゲットはステップ関数である：

入力は，によるたたみ込みを介して出力によって決定される：

正則化なしでは，予測される応答は信号に非常に近くなるが，計算された信号は振動が多い：

変動を正則化すると，はるかに滑らかな近似が得られる：

入力サイズの正則化も含めてよい：

変動正則化を使って破損した信号を平滑化する：

残差ノルムと変動ノルムの間のトレードオフをプロットする：

曲線が急激に曲がる場所の近くのの値を選ぶ：

全変動正則化を使ってジャンプで破損した信号を平滑化する：

パラメータで正則化する：

のより小さい値を使うとあまり滑らかではなくなるが，残差ノルムは小さくなる：

LASSO(L1)正則化を使って疎なフィットを求める（基底追跡）：

次は信号である：

目標は，何千ものガボール(Gabor)基底関数のほんの一部を使って信号を近似することである：

のとき，フィットはたった41個の基底要素で求まる：

誤差は極めて小さい：

基底の重要な要素が求まったら，これらの要素の最小二乗フィットを求めることで誤差が削減できる：

というより小さい値を使うと，フィットを求めるためにより多くの基底要素が必要になる：

誤差はさらに小さい：

トップへ