FoxH
FoxH[{{{a1,α1},…,{an,αn}},{{an+1,αn+1},…,{ap,αp}}},{{{b1,β1},…,{bm,βm}},{{bm+1,βm+1},…,{bq,βq}}},z]
is the Fox H-function ![]() .
.
Details


- Mathematical function, suitable for both symbolic and numerical manipulation.
- FoxH generalizes the MeijerG function and is defined by the Mellin–Barnes integral
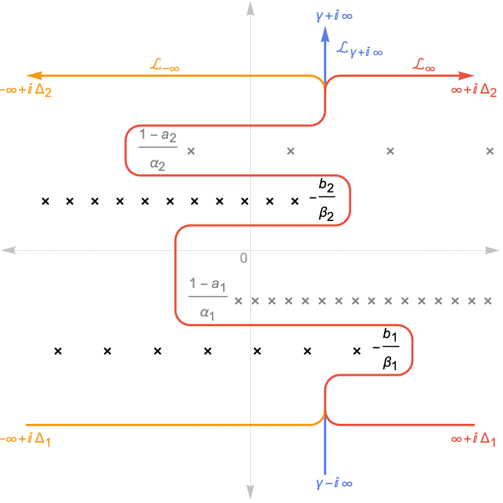
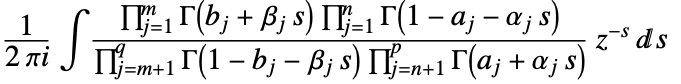 where
where 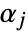 and
and 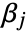 are positive real numbers and the integration is along a path
are positive real numbers and the integration is along a path 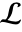 separating the poles of
separating the poles of 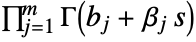 from the poles of
from the poles of 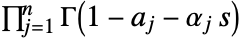 .
. - Three choices are possible for the path
 :
:
a. is a loop beginning at
is a loop beginning at 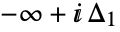 and ending at
and ending at 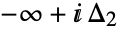 and encircling all the poles of
and encircling all the poles of 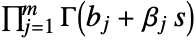 once in the positive direction.
once in the positive direction.
b.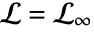 is a loop beginning at
is a loop beginning at 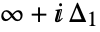 and ending at
and ending at 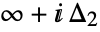 and encircling all the poles of
and encircling all the poles of 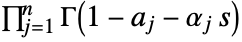 once in the negative direction.
once in the negative direction.
c.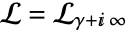 is a contour starting at the point
is a contour starting at the point 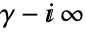 and going to
and going to 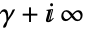 such that all the poles of
such that all the poles of 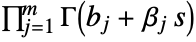 are separated from the poles of
are separated from the poles of 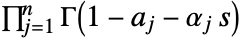 .
. - FoxH specializes to MeijerG if
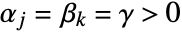 for
for 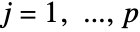 and
and 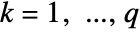 :
: 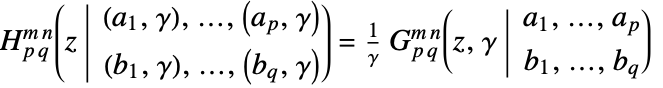 .
. - In many special cases, FoxH is automatically converted to other functions.
- FoxH can be evaluated for arbitrary complex parameters.
- FoxH can be evaluated to arbitrary numerical precision.
- FoxH automatically threads over lists. »
Examples
open allclose allBasic Examples (6)
Scope (28)
Numerical Evaluation (7)
The precision of the output tracks the precision of the input:
FoxH takes complex number parameters ![]() and
and ![]() :
:
FoxH takes complex number arguments:
Evaluate FoxH efficiently at high precision:
Compute the elementwise values of an array using automatic threading:
Or compute the matrix FoxH function using MatrixFunction:
Compute average-case statistical intervals using Around:
Specific Values (3)
Visualization (4)
Plot a family of FoxH functions:
ComplexContourPlot of FoxH[{{{},{}},{{{-1,1/2}},{}}, z]:
Use AbsArgPlot and ReImPlot to plot complex values of FoxH over the real numbers:
Plot FoxH as a function of parameters ![]() and
and ![]() :
:
Function Properties (5)
Differentiation (2)
First derivative with respect to z:
Higher-order derivative with respect to z:
Formula for the ![]()
![]() derivative of a specific FoxH with respect to z:
derivative of a specific FoxH with respect to z:
Integration (3)
Compute the indefinite integral using Integrate:
Series Expansions (4)
Get the series expansion of some FoxH function at the origin:
The first three approximations of this FoxH function around ![]() :
:
Find the series expansion of a general FoxH function at the origin:
Find the series expansion of a general FoxH function at Infinity:
Get the general term in the series expansion using SeriesCoefficient:
Applications (3)
Use FoxHReduce to get the representation of almost any mathematical function in terms of FoxH:
A root of the trinomial equation ![]() can be written in terms of FoxH:
can be written in terms of FoxH:
The roots of the general trinomial ![]() can also be expressed in terms of FoxH:
can also be expressed in terms of FoxH:
Express the PDF of StableDistribution in terms of FoxH for the case of ![]() :
:
Evaluate it and compare with the built-in PDF generated using StableDistribution:
Properties & Relations (2)
Use FunctionExpand to expand FoxH into simpler functions:
FoxHReduce returns FoxH representations of functions:
Possible Issues (3)
Neat Examples (1)
Many elementary and special functions are special cases of FoxH:
Text
Wolfram Research (2021), FoxH, Wolfram Language function, https://reference.wolfram.com/language/ref/FoxH.html (updated 2021).
CMS
Wolfram Language. 2021. "FoxH." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/FoxH.html.
APA
Wolfram Language. (2021). FoxH. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FoxH.html