FrobeniusNumber

FrobeniusNumber[{a1,…,an}]

gives the Frobenius number of a1,…,an.

Details

  • The Frobenius number of a1,…,an is the largest integer b for which the Frobenius equation a1x1+…+anxn==b has no non-negative integer solutions. The ai must be positive integers.
  • If the integers ai are not relatively prime, the result is Infinity.
  • If one of the ai is the integer 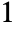, then the result is .
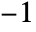  • If b is the Frobenius number of a1,…,an, then FrobeniusSolve[{a1,…,an},b] returns {}.

Examples

open allclose all

Basic Examples  (1)

The Frobenius number of 12, 16, 20, 27:

Applications  (2)

Make an array of Frobenius numbers:

Frobenius numbers of pairs:

Frobenius numbers of length-4 runs:

Properties & Relations  (1)

For a pair of relatively prime integers the Frobenius number has a closed form:

Check:

Wolfram Research (2007), FrobeniusNumber, Wolfram Language function, https://reference.wolfram.com/language/ref/FrobeniusNumber.html.

Text

Wolfram Research (2007), FrobeniusNumber, Wolfram Language function, https://reference.wolfram.com/language/ref/FrobeniusNumber.html.

CMS

Wolfram Language. 2007. "FrobeniusNumber." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FrobeniusNumber.html.

APA

Wolfram Language. (2007). FrobeniusNumber. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FrobeniusNumber.html

BibTeX

@misc{reference.wolfram_2024_frobeniusnumber, author="Wolfram Research", title="{FrobeniusNumber}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/FrobeniusNumber.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_frobeniusnumber, organization={Wolfram Research}, title={FrobeniusNumber}, year={2007}, url={https://reference.wolfram.com/language/ref/FrobeniusNumber.html}, note=[Accessed: 21-December-2024 ]}