WOLFRAM

Wolfram Language & System Documentation Center

FrobeniusNumber[{a1,…,an}]

给出 a1,…,an 的 Frobenius 数.

更多信息
Details and Options Details and Options
范例  
基本范例  
应用  
属性和关系  
参见
技术笔记
相关指南
相关链接
历史
按以下格式引用：

FrobeniusNumber

FrobeniusNumber[{a1,…,an}]

给出 a1,…,an 的 Frobenius 数.

更多信息

  • a1,…,an 的 Frobenius 数是使 Frobenius 方程 a1x1+…+anxn==b 没有非负整数解的最整数 b. ai 必须是正整数.
  • 如果整数 ai 不互质，结果是 Infinity.
  • 如果任一 ai 是整数 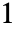，则结果是 .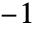
  • 如果 b 是 a1,…,an 的 Frobenius 数，则 FrobeniusSolve[{a1,…,an},b] 返回 {}.

范例

打开所有单元 关闭所有单元

基本范例  (1)

12、16、20、27 的 Frobenius 数：

应用  (2)

生成 Frobenius 数列表：

数字对的 Frobenius 数：

长度为 4 的列表的 Frobenius 数：

属性和关系  (1)

对于互质的整数对，Frobenius 数有一个解析表达式：

检测：

Wolfram Research (2007)，FrobeniusNumber，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FrobeniusNumber.html.

文本

Wolfram Research (2007)，FrobeniusNumber，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FrobeniusNumber.html.

CMS

Wolfram 语言. 2007. "FrobeniusNumber." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/FrobeniusNumber.html.

APA

Wolfram 语言. (2007). FrobeniusNumber. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FrobeniusNumber.html 年

BibTeX

@misc{reference.wolfram_2025_frobeniusnumber, author="Wolfram Research", title="{FrobeniusNumber}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/FrobeniusNumber.html}", note=[Accessed: 16-September-2025]}

BibLaTeX

@online{reference.wolfram_2025_frobeniusnumber, organization={Wolfram Research}, title={FrobeniusNumber}, year={2007}, url={https://reference.wolfram.com/language/ref/FrobeniusNumber.html}, note=[Accessed: 16-September-2025]}