FunctionPoles

FunctionPoles[f,x]

求变量为 x 的亚纯函数 f 的极点.

FunctionPoles[{f,cons},x]

给出 x 受约束条件 cons 限制的情况下 f 的极点.

更多信息和选项

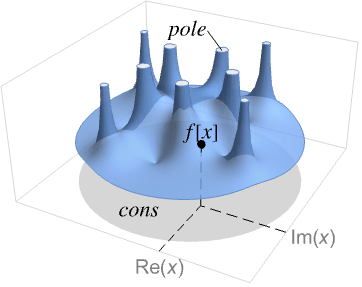
  • 函数的极点亦称为 "pole singularities".
  • 函数的极点通常用于计算复分析中函数的留数或计算幂级数的收敛半径.
  • 如果函数 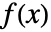有形为 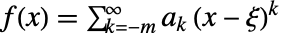的级数表示，则函数在 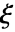处有重数 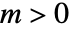的极点. 如果一个函数只有极点，那么该函数为亚纯函数.
  • FunctionPoles 返回数据对 {pole,multiplicity} 列表.
  • 对于满足约束条件 cons 的 x，函数 f 应为亚纯函数.
  • cons 可以含有等式、不等式或它们的逻辑组合.
  • 可给出以下选项：
  • Assumptions $Assumptions参数的假设条件
    GeneratedParameters C怎样命名生成的参数
    PerformanceGoal $PerformanceGoal优先考虑速度还是质量
  • 如果 FunctionPoles 无法确定极点的重数，则返回的某些极点的重数可能为 Indeterminate.

范例

打开所有单元关闭所有单元

基本范例  (2)

求有理函数的极点：

极点集可能是无限的：

范围  (6)

有理函数：

有无穷多个极点的函数：

求 TemplateBox[{x}, Abs]<=2 的极点：

解析函数没有极点：

在 处有可移除的奇点：

FunctionPoles 要求输入函数为亚纯函数：

时，函数为亚纯函数：

如果无法确定极点的重数，则返回的某些极点的重数可能为 Indeterminate：

选项  (3)

Assumptions  (1)

指定参数的条件：

GeneratedParameters  (1)

FunctionPoles 可能会引入新参数来表示解：

用 GeneratedParameters 控制如何命名参数：

PerformanceGoal  (1)

计算极点的重数可能要花费很长时间：

PerformanceGoal"Speed" 将限制计算重数所允许的时间：

两种情况下返回的极点相同：

第一种情况下，成功地算出了所有的重数：

第二种情况下，没有计算某些重数：

应用  (3)

对亚纯函数的奇点进行分类：

FunctionSingularities 给出极点的位置和可移除的奇异性：

在 处有一个双极点，在 处有一个单极点，在 处有一个可移除的奇点：

沿单位圆对 TemplateBox[{{{x, ^, 3}, -, {x, /, 3}}}, Gamma] 进行积分：

计算 在单位圆盘内的极点：

用留数定理计算积分：

与数值积分的结果相比较：

求 在 处的泰勒级数的收敛半径：

收敛半径等于到最近极点的距离：

尽管极点是复数，实数上的收敛也会受到影响：

由于 比 离极点更远， 处的收敛半径更大：

属性和关系  (4)

函数在极点处的绝对值的极限是 ：

用 Limit 计算极限：

函数在重数为 极点处的幂级数的第一项的指数为 ：

用 Series 计算级数：

用 Residue 求级数中指数为 的项的系数：

亚纯函数可以有的奇点只能是极点和可移除奇点：

用 FunctionSingularities 求所有奇点都满足的条件：

用 SolveValues 求奇点：

函数在 和 处有极点，在 处有可移除的奇点：

使用 FunctionPoles 找到函数的极点：

使用 Residue 找到两极的残差：

ResidueSum 给出所有极点的残差之和：

可能存在的问题  (2)

如果无法确定极点的重数，则返回的某些极点的重数可能为 Indeterminate：

FunctionPoles 有理化不精确的输入，然后将结果近似为输入精度：

结果可能取决于选择了哪些有理数：

在第一个例子中，有理化指数是一个整数；在第二个示例中则不是：

Wolfram Research (2021)，FunctionPoles，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FunctionPoles.html.

文本

Wolfram Research (2021)，FunctionPoles，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FunctionPoles.html.

CMS

Wolfram 语言. 2021. "FunctionPoles." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/FunctionPoles.html.

APA

Wolfram 语言. (2021). FunctionPoles. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FunctionPoles.html 年

BibTeX

@misc{reference.wolfram_2024_functionpoles, author="Wolfram Research", title="{FunctionPoles}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/FunctionPoles.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_functionpoles, organization={Wolfram Research}, title={FunctionPoles}, year={2021}, url={https://reference.wolfram.com/language/ref/FunctionPoles.html}, note=[Accessed: 21-November-2024 ]}