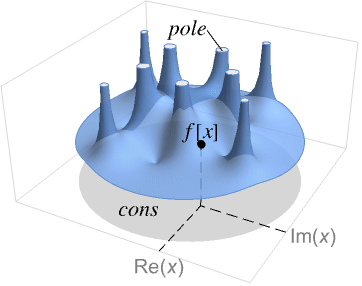
FunctionPoles
FunctionPoles[f,x]
finds the poles of the meromorphic function f with the variable x.
FunctionPoles[{f,cons},x]
gives the poles of f when x is restricted by the constraints cons.
Details and Options
- Function poles are also known as pole singularities.
- Function poles are often used to compute the residue of a function in complex analysis or to compute the radius of convergence for a power series.
- A function
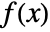has a pole singularity at 
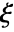with multiplicity 
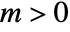if it has a series representation of the form 
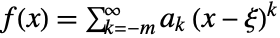. A function is meromorphic if it only has pole singularities. - FunctionPoles returns a list of pairs {pole,multiplicity}.
- The function f should be meromorphic for x satisfying the constraints cons.
- cons can contain equations, inequalities or logical combinations of these.
- The following options can be given:
-
Assumptions $Assumptions assumptions on parameters GeneratedParameters C how to name parameters that are generated PerformanceGoal $PerformanceGoal whether to prioritize speed or quality - Some of the returned poles may have Indeterminate multiplicity if FunctionPoles fails to determine their multiplicity.
Examples
open allclose allScope (6)
A function with infinitely many poles:
![TemplateBox[{x}, Abs]<=2](Files/FunctionPoles.en/6.png "TemplateBox[{x}, Abs]<=2"){kind=small}
Analytic functions have no poles:
has a removable singularity at 
:
FunctionPoles requires the input function to be meromorphic:
The function is meromorphic for 
:
Some of the returned poles may have Indeterminate multiplicity if determining the multiplicity fails:
Options (3)
GeneratedParameters (1)
FunctionPoles may introduce new parameters to represent the solution:
Use GeneratedParameters to control how the parameters are named:
PerformanceGoal (1)
Computing multiplicities of poles may take a long time:
PerformanceGoal"Speed" limits the time allowed for computation of multiplicity:
The poles returned in both cases are the same:
In the first case, all multiplicities are computed successfully:
Applications (3)
Classify singularities of a meromorphic function:
FunctionSingularities gives locations of poles and removable singularities:
has a double pole at 
, a single pole at 
and a removable singularity at 
:
Integrate ![TemplateBox[{{{x, ^, 3}, -, {x, /, 3}}}, Gamma]](Files/FunctionPoles.en/15.png "TemplateBox[{{{x, ^, 3}, -, {x, /, 3}}}, Gamma]"){kind=small}
along the unit circle:
Compute the poles of 
in the unit disk:
Compute the integral using the residue theorem:
Compare with the result of numeric integration:
Find the radius of convergence of the Taylor series of 
at 
:
The radius of convergence equals the distance to the nearest pole:
Even though the poles are complex, the convergence over the reals is affected:
Since 
is farther from the poles than 
, the convergence radius at 
is greater:
Properties & Relations (4)
The limit of the absolute value of a function at a pole is 
:
Use Limit to compute the limit:
The first term of the power series of a function at a pole of multiplicity 
has exponent 
:
Use Series to compute the series:
Use Residue to find the coefficient at the series term with exponent 
:
The only singularities a meromorphic function can have are poles and removable singularities:
Use FunctionSingularities to find a condition satisfied by all singularities:
Use SolveValues to find the singularities:
The function has poles at 
and 
and a removable singularity at 
:
Use FunctionPoles to find the poles of a function:
Use Residue to find the residues at the poles:
ResidueSum gives the sum of the residues at all poles:
Possible Issues (2)
Some of the returned poles may have Indeterminate multiplicity if determining the multiplicity fails:
FunctionPoles rationalizes inexact inputs and then approximates the result to the input precision:
The result may depend on which rational numbers are chosen:
In the first example, the rationalized exponent is an integer; in the second example, it is not:
Text
Wolfram Research (2021), FunctionPoles, Wolfram Language function, https://reference.wolfram.com/language/ref/FunctionPoles.html.
CMS
Wolfram Language. 2021. "FunctionPoles." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FunctionPoles.html.
APA
Wolfram Language. (2021). FunctionPoles. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FunctionPoles.html