ResidueSum

ResidueSum[f,z]

finds the sum of residues of the meromorphic function f with the variable z.

ResidueSum[{f,cons},z]

finds the sum of residues of f within the solution set of the constraints cons.

Details and Options

  • ResidueSum computes the sum of residues at all poles of f. The residue of f at a pole z0 is defined as the coefficient of 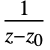in the Laurent expansion of f.
  • Sums of residues are often used to compute contour integrals using Cauchy's residue theorem.
  • The function f should be meromorphic for x satisfying the constraints cons.
  • cons can contain equations, inequalities or logical combinations of these.
  • The following options can be given:
  • Assumptions $Assumptionsassumptions on parameters
    GenerateConditions Automaticwhether to generate conditions on parameters
    PerformanceGoal $PerformanceGoalwhether to prioritize speed or quality

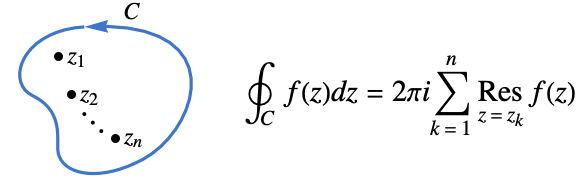
Examples

open allclose all

Basic Examples  (2)

Find the sum of residues of a rational function:

Find the sum of residues of in a disk:

Scope  (6)

Sum of residues of a rational function:

Sum of residues of a meromorphic function in a region:

Sum of residues at infinitely many poles may be finite:

Analytic functions have no poles:

has a removable singularity at :

ResidueSum requires the input function to be meromorphic:

The function is meromorphic for :

Options  (4)

Assumptions  (1)

Specify conditions on parameters:

GenerateConditions  (2)

By default, ResidueSum may generate conditions on symbolic parameters:

With GenerateConditionsNone, ResidueSum fails instead of giving a conditional result:

This returns a conditionally valid result without stating the condition:

By default, conditions that are generically true are not reported:

With GenerateConditions->True, all conditions are reported:

PerformanceGoal  (1)

Use PerformanceGoal to avoid potentially expensive computations:

The default setting uses all available techniques to try to produce a result:

Applications  (1)

Integrate along the unit circle:

Compute the sum of residues of in the unit disk:

Compute the integral using the residue theorem:

Compare with the result of numeric integration:

Properties & Relations  (3)

Use FunctionPoles to find the poles of a function:

Use Residue to find the residues at the poles:

ResidueSum gives the sum of the residues at all poles:

Use FunctionMeromorphic to test whether a function is meromorphic:

Compute the sum of residues in a region where the function is meromorphic:

Use FunctionAnalytic to test whether a function is complex analytic:

Sum of residues of an analytic function is zero:

Wolfram Research (2022), ResidueSum, Wolfram Language function, https://reference.wolfram.com/language/ref/ResidueSum.html.

Text

Wolfram Research (2022), ResidueSum, Wolfram Language function, https://reference.wolfram.com/language/ref/ResidueSum.html.

CMS

Wolfram Language. 2022. "ResidueSum." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ResidueSum.html.

APA

Wolfram Language. (2022). ResidueSum. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ResidueSum.html

BibTeX

@misc{reference.wolfram_2025_residuesum, author="Wolfram Research", title="{ResidueSum}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/ResidueSum.html}", note=[Accessed: 21-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_residuesum, organization={Wolfram Research}, title={ResidueSum}, year={2022}, url={https://reference.wolfram.com/language/ref/ResidueSum.html}, note=[Accessed: 21-February-2025 ]}