FunctionAnalytic[f,x]
tests whether ![]() is an analytic function for x∈Reals.
is an analytic function for x∈Reals.
FunctionAnalytic[f,x,dom]
tests whether ![]() is an analytic function for x∈dom.
is an analytic function for x∈dom.
FunctionAnalytic[{f1,f2,…},{x1,x2,…},dom]
tests whether ![]() are analytic functions for x1,x2,…∈dom.
are analytic functions for x1,x2,…∈dom.
FunctionAnalytic[{funs,cons},xvars,dom]
tests whether ![]() are analytic functions for xvars in an open set containing the solutions of the constraints cons over the domain dom.
are analytic functions for xvars in an open set containing the solutions of the constraints cons over the domain dom.


FunctionAnalytic
FunctionAnalytic[f,x]
tests whether ![]() is an analytic function for x∈Reals.
is an analytic function for x∈Reals.
FunctionAnalytic[f,x,dom]
tests whether ![]() is an analytic function for x∈dom.
is an analytic function for x∈dom.
FunctionAnalytic[{f1,f2,…},{x1,x2,…},dom]
tests whether ![]() are analytic functions for x1,x2,…∈dom.
are analytic functions for x1,x2,…∈dom.
FunctionAnalytic[{funs,cons},xvars,dom]
tests whether ![]() are analytic functions for xvars in an open set containing the solutions of the constraints cons over the domain dom.
are analytic functions for xvars in an open set containing the solutions of the constraints cons over the domain dom.
Details and Options

- Complex analytic functions are also known as holomorphic functions.
- A function
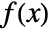 is analytic in an open set
is analytic in an open set 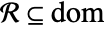 if for all y∈ℛ there is an
if for all y∈ℛ there is an 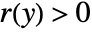 and a sequence
and a sequence 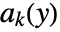 such that for all
such that for all ![TemplateBox[{{x, -, y}}, Abs]<r(y) TemplateBox[{{x, -, y}}, Abs]<r(y)](Files/FunctionAnalytic.en/9.png) ,
, 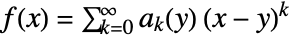 .
. - A function
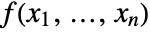 is analytic in an open set
is analytic in an open set 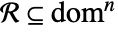 if for all
if for all 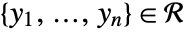 there is an
there is an 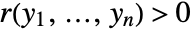 and a sequence
and a sequence 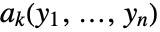 such that for all
such that for all ![TemplateBox[{{{, {{{x, _, 1}, -, {y, _, 1}}, ,, ..., ,, {{x, _, n}, -, {y, _, n}}}, }}}, Norm]<r(y_1,...,y_n) TemplateBox[{{{, {{{x, _, 1}, -, {y, _, 1}}, ,, ..., ,, {{x, _, n}, -, {y, _, n}}}, }}}, Norm]<r(y_1,...,y_n)](Files/FunctionAnalytic.en/16.png) ,
, ![f(x_1,...,x_n)=sum_(k in TemplateBox[{}, NonNegativeIntegers]^n)a_k(y_1,...,y_n)(x_1-y_1)^(k_1) ... (x_n-y_n)^(k_n) f(x_1,...,x_n)=sum_(k in TemplateBox[{}, NonNegativeIntegers]^n)a_k(y_1,...,y_n)(x_1-y_1)^(k_1) ... (x_n-y_n)^(k_n)](Files/FunctionAnalytic.en/17.png) .
. - If funs contains parameters other than xvars, the result is typically a ConditionalExpression.
- Possible values for dom are Reals and Complexes. The default is Reals.
- If dom is Reals, then all variables, parameters, constants and function values are restricted to be real.
- cons can contain inequalities or logical combinations of these.
- The following options can be given:
-
Assumptions $Assumptions assumptions on parameters GenerateConditions True whether to generate conditions on parameters PerformanceGoal $PerformanceGoal whether to prioritize speed or quality - Possible settings for GenerateConditions include:
-
Automatic nongeneric conditions only True all conditions False no conditions None return unevaluated if conditions are needed - Possible settings for PerformanceGoal are "Speed" and "Quality".
Examples
open all close allBasic Examples (4)
Scope (6)
Options (4)
Assumptions (1)
FunctionAnalytic cannot find the answer for arbitrary values of the parameter ![]() :
:
With the assumption that ![]() , FunctionAnalytic succeeds:
, FunctionAnalytic succeeds:
GenerateConditions (2)
By default, FunctionAnalytic may generate conditions on symbolic parameters:
With GenerateConditions->None, FunctionAnalytic fails instead of giving a conditional result:
This returns a conditionally valid result without stating the condition:
By default, all conditions are reported:
With GenerateConditions->Automatic, conditions that are generically true are not reported:
PerformanceGoal (1)
Use PerformanceGoal to avoid potentially expensive computations:
The default setting uses all available techniques to try to produce a result:
Applications (11)
Classes of Analytic Functions (6)
Sin, Cos and Exp are analytic:
These functions are analytic in the complex plane as well:
Visualize these functions over ![]() :
:
Functions that are analytic in the plane are called entire functions and can be considered infinite-degree polynomials:
No discontinuous function is analytic:
Visualize some of the preceding functions:
Some continuous functions are not analytic, like the real absolute value function RealAbs:
The problem with RealAbs is the "kink" at the origin:
The complex absolute value function Abs is analytic nowhere in the complex plane:
It suffers from a different problem than RealAbs, namely it is nowhere differentiable:
The reciprocal of an analytic function ![]() is analytic wherever
is analytic wherever ![]() :
:
Thus, rational functions may or may not be continuous over the reals:
However, as every nonconstant polynomial has a root in the plane, rational functions are never analytic on ![]() :
:
Instead, rational functions are the prototype of the larger class of meromorphic functions in the complex plane:
Visualizing the function in the complex plane shows the blowup at ![]() :
:
As Cot and Csc are rational functions of Sin and Cos, they are analytic when sine is nonzero:
Visualize the functions along with sine:
Since sine's only zeros are on the real line, this means the Cot and Csc are analytic except on the multiples of ![]() :
:
Similarly, Tan and Sec are continuous when cosine is nonzero:
This same principle applies to the hyperbolic trigonometric functions Coth and Csch:
But as the zeros of Cosh and Sinh lie on the imaginary axis, more exclusions are needed for analyticity over ![]() :
:
Plots of the hyperbolic functions are just rotations by ![]() along with a phase shift by the same amount:
along with a phase shift by the same amount:
The compositions of analytic functions are analytic:
Multivariate polynomials are analytic over the reals and complexes:
So are multivariate polynomials in entire functions:
Rational multivariate functions may or may not be analytic over the reals:
They are always nonanalytic over the complexes:
By composing with analytic univariate functions, many more analytic functions can be generated:
Calculus (5)
Analytic functions can be represented by power series:
In this case, the sum converges for all values of ![]() :
:
Consider the following function:
It is analytic on the open disk of radius 5:
Therefore it can be expressed as a power series about any point in the disk, say ![]() :
:
However, this sum does not converge for all values of ![]() :
:
Substituting a value of ![]() outside this range produces a divergent sum:
outside this range produces a divergent sum:
Visualize the function along with the domains of analyticity and convergence:
The integral of an analytic function around a close contour is zero:
The following integral is nonzero, so Log cannot be analytic:
Visualize the functions and the contour:
If ![]() and
and ![]() are analytic in a region
are analytic in a region ![]() in the complex plane,
in the complex plane, ![]() only has simple zeros and
only has simple zeros and ![]() is nonzero. A sum over the zeros of
is nonzero. A sum over the zeros of ![]() can be computed as
can be computed as ![]() . Consider
. Consider ![]() :
:
This function is analytic in a disk of radius 4:
Let ![]() . It is analytic and nonzero in the disk of radius 4:
. It is analytic and nonzero in the disk of radius 4:
The function ![]() has two simple roots within the disk, at
has two simple roots within the disk, at ![]() and
and ![]() :
:
Thus, the sum is easy to compute:
The integral gives the same answer:
Differential equations with analytic coefficients have solutions that are analytic at most points, which makes series solutions a viable method of approach. Consider the following differential equation:
There is no closed-form solution to this equation:
However, all coefficients are analytic:
Thus, a series solution can be found using AsymptoticDSolveValue:
However, its first derivative is not continuous:
While ![]() goes smoothly to zero, its derivative oscillates wildly at the origin:
goes smoothly to zero, its derivative oscillates wildly at the origin:
Properties & Relations (7)
An analytic function is differentiable arbitrarily many times:
Use D to compute derivatives:
An analytic function can be expressed as a Taylor series at each point of its domain:
Use Series to compute initial terms of Taylor series:
The resulting polynomial approximates ![]() near
near ![]() :
:
Zeros of an analytic function cannot have an accumulation point in the domain:
Zeros of ![]() have an accumulation point at
have an accumulation point at ![]() :
:
![]() is continuous, but not analytic:
is continuous, but not analytic:
![]() is analytic if
is analytic if ![]() is excluded from the domain:
is excluded from the domain:
An analytic function can have only finitely many zeros in a closed and bounded region:
Use Solve to find the roots of ![]() in the unit disk:
in the unit disk:
Use FunctionContinuous to check whether a function is continuous:
Continuous functions may not be analytic:
Analytic functions are continuous:
Use FunctionMeromorphic to check whether a function is meromorphic:
Meromorphic functions may not be complex analytic:
A quotient of complex analytic functions is meromorphic:
Sum of residues of an analytic function is zero:
Use ResidueSum to verify this property:
Possible Issues (3)
See Also
FunctionContinuous FunctionMeromorphic FunctionSingularities FunctionDiscontinuities Series
Function Repository: FunctionDifferentiability PossiblyDifferentiableQ
Related Guides
History
Text
Wolfram Research (2020), FunctionAnalytic, Wolfram Language function, https://reference.wolfram.com/language/ref/FunctionAnalytic.html.
CMS
Wolfram Language. 2020. "FunctionAnalytic." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FunctionAnalytic.html.
APA
Wolfram Language. (2020). FunctionAnalytic. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FunctionAnalytic.html
BibTeX
@misc{reference.wolfram_2025_functionanalytic, author="Wolfram Research", title="{FunctionAnalytic}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/FunctionAnalytic.html}", note=[Accessed: 17-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_functionanalytic, organization={Wolfram Research}, title={FunctionAnalytic}, year={2020}, url={https://reference.wolfram.com/language/ref/FunctionAnalytic.html}, note=[Accessed: 17-January-2026]}