GCD

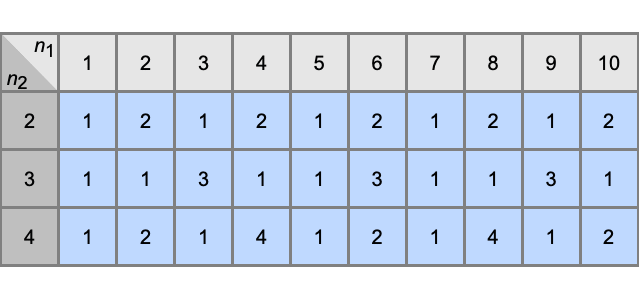
GCD[n1,n2,…]

niの最大公約数を返す．

詳細

  • GCDは，最大公約数として知られている．
  • 記号操作・数値操作の両方に適した数学関数である．
  • GCD[n1,n2,…]は整数 n1,n2,…のそれぞれを割る最大の正の整数である．
  • 有理数 riについて，GCD[r1,r2,…]はすべての ri/r が整数となる最大の有理数 r を返す．
  • GCDはガウス整数に使うことができる．

例題

すべて開くすべて閉じる

例  (2)

数の集合の最大公約数を求める：

ある数との最大公約数をプロットする：

スコープ  (11)

数値評価  (7)

GCDは整数に使うことができる：

ガウス整数：

実有理数：

複素有理数：

正の整数については1引数の形は恒等式である：

引数がない形は0である：

大きい整数について計算する：

GCDは要素単位でリストに縫い込まれる：

記号演算  (4)

TraditionalFormによる表示：

不等式を簡約する：

方程式を解く：

式を簡約する：

アプリケーション  (11)

基本的なアプリケーション  (3)

最初の100個の整数ペアの最大公約数の表：

2つの整数の最大公約数を可視化する：

フィボナッチ(Fibonacci)数：

正の整数のGCDを計算する：

以下と比較する：

整数論  (8)

EulerPhiを使ってGCDを計算する：

Floorを使ってGCDを計算する：

連続する数の「ボール」の最大公約数の平均をプロットする：

線形合同方程式が可解となる条件：

最初の100個の数のペアのうち互いに素であるものの割合を求める：

結果はに近い：

ペアごとの最大公約数の行列の行列式は，オイラー(Euler)のトーシェント関数に関連している：

k 個のランダムな整数が最大公約数 d を持つ確率はである：

以下と比較する：

GCDを含む式を簡約する：

特性と関係  (8)

a と b の公約数はどれも の約数である：

素数のGCDはである：

素数ベキ表現 のGCD：

ExtendedGCDは，整数 a と b について を満足する整数 x と y を与える：

CoprimeQを使って自明な最大公約数をチェックする：

フィボナッチ(Fibonacci)数の最大公約数特性：

非負の整数 a，b，n は を満足する：

GCDは可換である ：

GCDは結合法則を満たす ：

GCDは分配法則を満たす ：

考えられる問題  (3)

符号は無視される：

引数は明示的な整数でなければならない：

GCDはその引数をソートする：

インタラクティブな例題  (1)

3つの数の最大公約数を可視化する：

おもしろい例題  (4)

GCDのフーリエ変換の引数をプロットする：

GCDのフーリエ変換の絶対値をプロットする：

GCDのウラム(Ulam)螺線をプロットする：

有理数での最大公約数を形作る：

Wolfram Research (1988), GCD, Wolfram言語関数， https://reference.wolfram.com/language/ref/GCD.html （1999年に更新）.

テキスト

Wolfram Research (1988), GCD, Wolfram言語関数， https://reference.wolfram.com/language/ref/GCD.html （1999年に更新）.

CMS

Wolfram Language. 1988. "GCD." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 1999. https://reference.wolfram.com/language/ref/GCD.html.

APA

Wolfram Language. (1988). GCD. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GCD.html

BibTeX

@misc{reference.wolfram_2024_gcd, author="Wolfram Research", title="{GCD}", year="1999", howpublished="\url{https://reference.wolfram.com/language/ref/GCD.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_gcd, organization={Wolfram Research}, title={GCD}, year={1999}, url={https://reference.wolfram.com/language/ref/GCD.html}, note=[Accessed: 21-November-2024 ]}