GaborWavelet

表示频率为6的 Gabor 小波.

GaborWavelet[w]

表示频率为 w 的 Gabor 小波.

更多信息

GaborWavelet 定义一个复合非正交小波族.
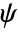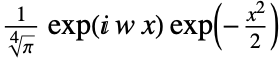小波函数 () 由给出.
GaborWavelet 可与 ContinuousWaveletTransform 和 WaveletPsi 等函数联合使用.

范例

打开所有单元关闭所有单元

基本范例 (1)

小波函数：

范围 (2)

GaborWavelet 用于 ContinuousWaveletTransform:

用 WaveletScalogram 得到小波系数的时间尺度表示：

使用 InverseWaveletTransform 重建信号：

作为一个频率为 w 的函数的小波函数：

应用 (1)

求解（resolve)一个频率为10赫兹的余弦波：

对数据进行连续小波变换：

由变换得到的(resolve)频率为尺度的倒数：

绘制 WaveletScalogram 的图形，以验证10赫兹的频率被第七个倍频程吸收（resolve)：

属性和关系 (4)

一定频率的 GaborWavelet 与 MorletWavelet 相似：

小波函数及其傅立叶变换：

GaborWavelet 没有尺度函数：

GaborWavelet[w] 的中央频率近似为 w：

计算频率参数为的小波函数：

绘制一个小波函数的实部，该小波函数与一条正弦曲线在中央频率处重叠：

虚部：

顶部

启用 JavaScript 与内容交互以及在 Wolfram 网站提交申请。了解更多