GaborWavelet
周波数6のGaborウェーブレットを表す．
GaborWavelet[w]
周波数 w のGaborウェーブレットを表す．
詳細
- GaborWaveletは複素非直交ウェーブレット族を定義する．
- ウェーブレット関数(
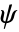)は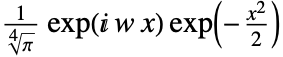 
で与えられる． - GaborWaveletは，ContinuousWaveletTransform，WaveletPsi等の関数で使うことができる．
例題
すべて開く すべて閉じるスコープ (2)
GaborWaveletを使ってContinuousWaveletTransformを行うことができる：
WaveletScalogramを使ってウェーブレット係数のタイムスケール表現を得ることができる：
InverseWaveletTransformを使って信号を再構築する：
アプリケーション (1)
WaveletScalogramをプロットして10Hzの周波数が第7オクターブによって分解されたことを確かめる：
特性と関係 (4)
ある種の周波数を伴うGaborWaveletはMorletWaveletに似ている：
GaborWaveletはスケーリング関数を持たない：
GaborWavelet[w]の中心周波数はほぼ w である：
テキスト
Wolfram Research (2010), GaborWavelet, Wolfram言語関数， https://reference.wolfram.com/language/ref/GaborWavelet.html.
CMS
Wolfram Language. 2010. "GaborWavelet." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GaborWavelet.html.
APA
Wolfram Language. (2010). GaborWavelet. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GaborWavelet.html