GeodesicPolyhedron
gives the order‐n geodesic polyhedron.
GeodesicPolyhedron["poly",n]
gives the order‐n geodesic polyhedron based on the polyhedron "poly".
Details and Options

- GeodesicPolyhedron is also known as icosphere.
- GeodesicPolyhedron is typically used to approximate a sphere.
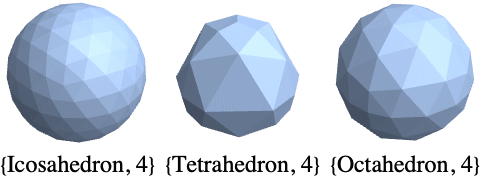
- GeodesicPolyhedron["poly",n] gives a Polyhedron generated by subdividing faces of "poly" and projecting the new points onto the surface of the unit sphere.
- Possible values of "poly" include "Tetrahedron", "Octahedron" and "Icosahedron".
- GeodesicPolyhedron[n] is effectively equivalent to GeodesicPolyhedron["Icosahedron",n].
Examples
open allclose allScope (6)
Basic Uses (5)
Generate an equilateral tetrahedron, octahedron, icosahedron, etc.:
Color directives specify the face colors of geodesic polyhedrons:
FaceForm and EdgeForm can be used to specify the styles of the interior and boundary:
Geodesic polyhedra are three-dimensional geometric regions:
Applications (2)
Properties & Relations (5)
A geodesic polyhedron is convex:
A geodesic polyhedron is simple:
The OuterPolyhedron of a geodesic polyhedron is itself:
Geodesic polyhedrons do not have holes:
The number of faces of a geodesic polyhedron from Icosahedron:
The number of vertices of a geodesic polyhedron from Icosahedron:
Text
Wolfram Research (2022), GeodesicPolyhedron, Wolfram Language function, https://reference.wolfram.com/language/ref/GeodesicPolyhedron.html.
CMS
Wolfram Language. 2022. "GeodesicPolyhedron." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GeodesicPolyhedron.html.
APA
Wolfram Language. (2022). GeodesicPolyhedron. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GeodesicPolyhedron.html