GeometricOptimization
GeometricOptimization[f,cons,vars]
正の多項式制約 cons に従って正の多項目的関数を最小化する変数 vars の正の値を求める.
GeometricOptimization[{a0,b0},{{a1,b1},…},{aeq,beq}]
不等式制約 ![]() と線形等式制約
と線形等式制約 ![]() に従って
に従って ![]() を最小化する正のベクトル x=yを求める.
を最小化する正のベクトル x=yを求める.
GeometricOptimization[…,"prop"]
解のどの特性"prop"を返すべきかを指定する.
詳細とオプション




- 幾何学的最適化は幾何計画法(GP)および混合整数幾何計画法(MIGP)としても知られている.
- 幾何学的最適化は,面積,体積,電力等の最小化にしばしば使われる.
- 幾何学的最適化は主問題を解く
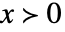 を求める.
を求める. -
最小化 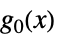
制約条件 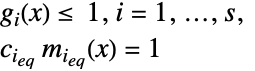
ただし 
- 単項式は,
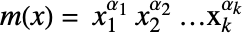 (ただし
(ただし 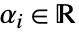 )のベキの積である.正多項式は単項式
)のベキの積である.正多項式は単項式 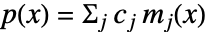 (ただし
(ただし 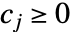 )の正の和である.
)の正の和である. - 一般化された正多項式
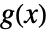 は,正多項式または一般化された正多項式の組合せである.
は,正多項式または一般化された正多項式の組合せである. -
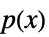
正多項式 
一般化された正多項式の和 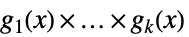
一般化された正多項式の積 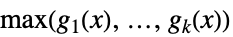
一般化された正多項式の最大値 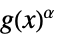
一般化された正多項式の正の実数ベキ - 正多項式
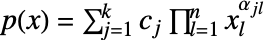 は,以下のように,変換
は,以下のように,変換 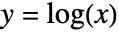 によって
によって 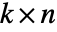 行列
行列 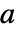 (
(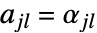 )と
)と 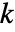 -ベクトル
-ベクトル 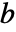 (
(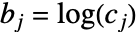 )に対応する.
)に対応する. -
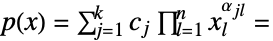
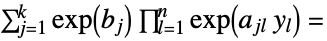
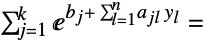
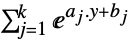
- 同様の問題の定式化は
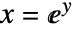 を求めることである.ただし,
を求めることである.ただし,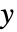 が問題を解く.
が問題を解く. -
最小化 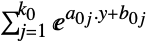
制約条件 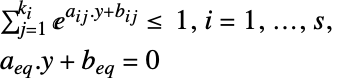
ただし 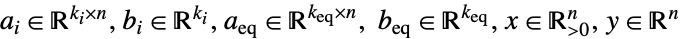
- GeometricOptimization[{a0,b0},{{a1,b1},…},{aeq,beq}]の aiは
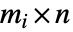 行列,biは
行列,biは 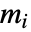 ベクトル,aeqは
ベクトル,aeqは 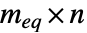 行列,
行列,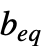 は
は 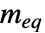 ベクトルである.等式制約がない場合は,{aeq,beq}は{}で与えることも省略することもできる.
ベクトルである.等式制約がない場合は,{aeq,beq}は{}で与えることも省略することもできる. - 主最小化問題には関連する最大化問題(ラグランジュ双対問題)がある.双対最大値は常に主最小値以下なので,下界を与える.双対マキシマイザは,制約条件の変化に対する最小値の感度を含む主問題の情報を与える.
- 幾何学的最適化問題は双対問題を持つ.
-
最大化 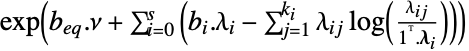
制約条件 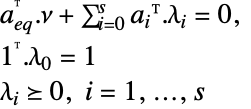
ただし 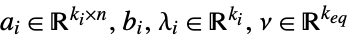
- 錐最適化については強双対性が常に存在するので,主最小化問題に解がある場合は双対最大化問題にも解があり,双対最大値は主最小値に等しい.
- 次は,使用可能な解の特性"prop"である.
-
"PrimalMinimizer" 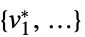
f を最小化する vars={v1,…}の値のリスト "PrimalMinimizerRules" 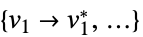
vars={v1,…}の値を最小化する規則 "PrimalMinimizerVector" 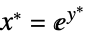
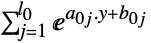 を最小化するベクトル
を最小化するベクトル"PrimalMinimumValue" 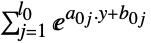
最小値 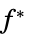
"DualMaximizer" 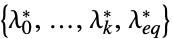
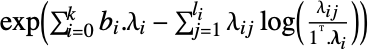 を最大化するベクトル
を最大化するベクトル 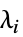 のリスト
のリスト"DualMaximumValue" 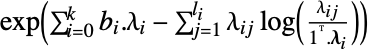
双対最大値 "DualityGap" 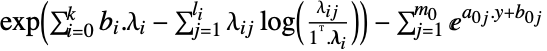
双対最適値と主最適値の差 "Slack" 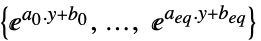
正多項式項の各単項式の値を与えるベクトル "ConstraintSensitivity" 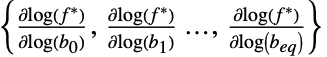
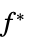 の制約摂動に対する感度
の制約摂動に対する感度"ConstraintMatrices" 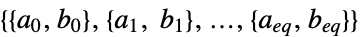
項 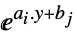 についての行列
についての行列"ObjectiveFunction" 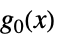
目的関数 "GeometricConstraints" 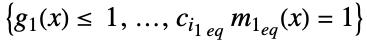
幾何学的制約のリスト {"prop1","prop2",…} いくつかの解の特性 - 次は,使用可能なオプションである.
-
MaxIterations Automatic 使用する反復の最大数 Method Automatic 使用するメソッド PerformanceGoal $PerformanceGoal パフォーマンスのどの面を最適化するか Tolerance Automatic 内部比較に使用する許容範囲 - 計算はMachinePrecisionに限定される.
例題
すべて開くすべて閉じるスコープ (12)
基本的な用法 (4)
主モデル特性 (3)
双対モデル特性 (2)
ConicOptimizationを使った定式化は,凸項 ![]() を中間変数
を中間変数 ![]() で置換し,以前使った双対指数錐制約に等しい制約条件
で置換し,以前使った双対指数錐制約に等しい制約条件 ![]() を加える.
を加える.![]() は
は![]() を必要とする.
を必要とする.
![]() と
と ![]() は"DualMaximizer"特性からより簡単に得ることができる:
は"DualMaximizer"特性からより簡単に得ることができる:
GeometricOptimizationには強双対性があるので,双対最大値は主最小値に等しい.その差は双対性のギャップと言われる:
すべての項が単項式なので,行列 ![]() のどれもが1行であり,双対ベクトル
のどれもが1行であり,双対ベクトル ![]() には1つの要素しかない.したがって
には1つの要素しかない.したがって![]() である.
である.![]() を最大化することは
を最大化することは![]() を最小化することに等しい.また,指数関数が単調増加関数なので,これは
を最小化することに等しい.また,指数関数が単調増加関数なので,これは![]() を最小化することに等しい.したがって,双対問題は以下のように解くことができる:
を最小化することに等しい.したがって,双対問題は以下のように解くことができる:
感度特性 (3)
箱のコストを100ドル未満にするという制約条件に従って,縦 ![]() ,横
,横 ![]() ,高さ
,高さ ![]() の開放箱の体積を最大にする.底面のコストは単位面積あたり10ドルで,側面のコストは単位面積当たり1ドルである:
の開放箱の体積を最大にする.底面のコストは単位面積あたり10ドルで,側面のコストは単位面積当たり1ドルである:
底面のコストを10%下げた場合に箱の体積が相対的にどのように変化するかを推測する:
底面のコストの内訳は,第2要素の最初の部分である(第1要素は目的関数に相当する).![]() なので感度は打ち消される:
なので感度は打ち消される:
縦 ![]() ,横
,横 ![]() ,高さ
,高さ ![]() の箱の天面と底面あるいは側面についての制約条件を変えた場合に,この箱の最大体積が相対的にどのように変化するかを求める.体積を最大にすることは体積の逆数を最小にすることと同じである:
の箱の天面と底面あるいは側面についての制約条件を変えた場合に,この箱の最大体積が相対的にどのように変化するかを求める.体積を最大にすることは体積の逆数を最小にすることと同じである:
側面の総面積を ![]() 以下に,天面と底面の面積を
以下に,天面と底面の面積を ![]() 以下に制限する:
以下に制限する:
面積の条件に関連するのは2番目と3番目である(最初のものは目的関数に関連している):
これは,![]() が少し変化しても{α,β}={38,47}の体積は変化しないことを意味する:
が少し変化しても{α,β}={38,47}の体積は変化しないことを意味する:
![]() の2つの成分は相対する2組の側面から来ているので,体積の相対変化の合計は以下のようになる:
の2つの成分は相対する2組の側面から来ているので,体積の相対変化の合計は以下のようになる:
アプリケーション (16)
幾何学的問題 (4)
面積4の長方形の対角線の長さを最小にする.ただし,横に縦の3倍を加えたものが7以下になるようにする:
体積 ![]() の球状のスクープを入れるアイスクリームコーンをデザインする.スクープとコーンの半径は同じであるとする.アイスクリームが溶けたときにコーンにスクープ全体が入るようにしてコーンの表面積を最小にする:
の球状のスクープを入れるアイスクリームコーンをデザインする.スクープとコーンの半径は同じであるとする.アイスクリームが溶けたときにコーンにスクープ全体が入るようにしてコーンの表面積を最小にする:
![]() の違いがあまりない場合は,
の違いがあまりない場合は,![]() のときの表面積は以下で近似される:
のときの表面積は以下で近似される:
予想通り,それは球である.軸の長さについての制限を加えると結果が変わる:
どの次元もその差が2倍以上にはならず,側面,天面,底面の総面積についての制約条件がある中で,縦 ![]() ,横
,横 ![]() ,高さ
,高さ ![]() の箱の体積を最大にする:
の箱の体積を最大にする:
側面の総面積 ![]() と底面と天面の合計
と底面と天面の合計 ![]() が与えられると体積を返す関数を定義する:
が与えられると体積を返す関数を定義する:
行列問題 (2)
貯蔵タンクの設計 (1)
フロアプラン (1)
縦横比,長方形間の距離,相対的な配置の制約がある指定された面積の ![]() 個の長方形を囲む,全体の面積が最小の長方形フロアを計設計する.
個の長方形を囲む,全体の面積が最小の長方形フロアを計設計する.
大きい長方形を Rectangle[{0,0},{H,W}]で,個々の小さい長方形を ri=Rectangle[{xi,yi},{xi+wi,yi+hi}], i=1,…,n で表す.
各長方形の縦横比 ![]() を,
を,![]() となるように
となるように![]() から
から ![]() (ただし
(ただし ![]() )に制限する.
)に制限する.
相対配置は,水平配置 ![]() と垂直配置
と垂直配置 ![]() の2つの有向グラフで表すことができる.ij という辺がある場合は riは rjの左(または下)にならなければならない:
の2つの有向グラフで表すことができる.ij という辺がある場合は riは rjの左(または下)にならなければならない:
長方形間の最小スペースを ![]() とする.
とする.![]() に辺 ij があるとき,長方形
に辺 ij があるとき,長方形 ![]() は
は ![]() となるように長方形
となるように長方形 ![]() の左にならなければならない.
の左にならなければならない.![]() に辺 ij があるとき,長方形
に辺 ij があるとき,長方形 ![]() は
は ![]() となるように長方形
となるように長方形 ![]() の下にならなければならない.次の関数で,グラフを横断しフロアの端になる長方形を説明することができる:
の下にならなければならない.次の関数で,グラフを横断しフロアの端になる長方形を説明することができる:
配置グラフ,面積,![]() および
および ![]() が与えられると,GeometricOptimizationを使う関数で規則を組み合せることができる:
が与えられると,GeometricOptimizationを使う関数で規則を組み合せることができる:
次は,最初の長方形が他の2つの長方形の左側になり2番目の長方形が3番目の長方形の下になるような,3つの長方形の相対配置を表すグラフである:
構造最適化の問題 (3)
垂直荷重 ![]() または水平荷重
または水平荷重 ![]() に従う最小重量のトラスを求める.トラスのバーは内半径
に従う最小重量のトラスを求める.トラスのバーは内半径 ![]() ,外半径
,外半径 ![]() ,密度
,密度 ![]() の中空のパイプである:
の中空のパイプである:
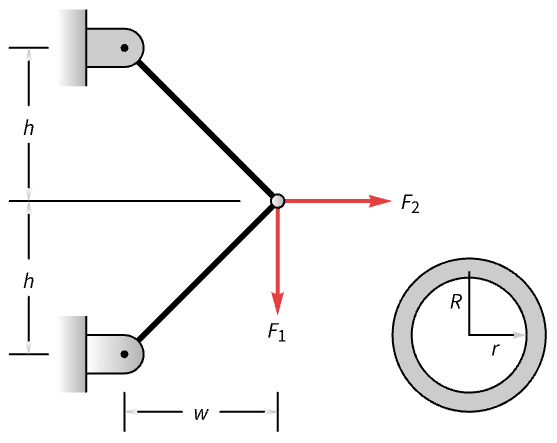
バーの長さはトラスの高さ ![]() と幅
と幅 ![]() を使って定義される.断面積は
を使って定義される.断面積は ![]() である.目的は重みを最小にすることである:
である.目的は重みを最小にすることである:
垂直荷重 ![]() が適用された場合に各バーにかかる力は以下の通りである:
が適用された場合に各バーにかかる力は以下の通りである:
水平荷重 ![]() 適用された場合に各バーにかかる力は以下の通りである:
適用された場合に各バーにかかる力は以下の通りである:
バーにかかる力の合計は最大許容力 ![]() を超えてはならない.ただし,
を超えてはならない.ただし,![]() は最大許容応力である:
は最大許容応力である:
チューブは最低でも壁の厚さがなければならない.これは,![]() (ただし
(ただし ![]() )で達成できる.バーの面積と半径の関係は
)で達成できる.バーの面積と半径の関係は ![]() であるが,これは単項関数ではない.
であるが,これは単項関数ではない.![]() と制約条件
と制約条件 ![]() を使うと,結果の制約条件は単項式になる:
を使うと,結果の制約条件は単項式になる:
垂直荷重 ![]() に従う最小重量のトラスを求める.トラスの高さ
に従う最小重量のトラスを求める.トラスの高さ ![]() と幅
と幅 ![]() は既知である.接合部
は既知である.接合部 ![]() の垂直位置は未知である:
の垂直位置は未知である:
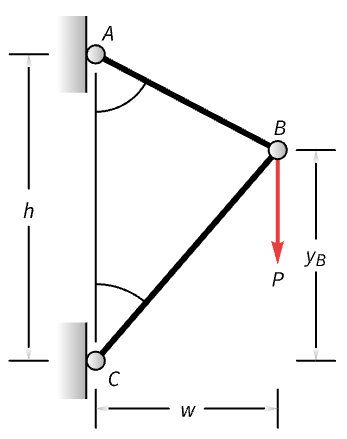
![]() を,それぞれバー
を,それぞれバー![]() および
および![]() の断面積,
の断面積,![]() をバーの密度とする.トラスの重みは以下で与えられる:
をバーの密度とする.トラスの重みは以下で与えられる:
バー![]() は伸長されている.
は伸長されている.![]() を材料の引張応力とする.バー
を材料の引張応力とする.バー![]() にかかる力は最大許容力を超えてはならない:
にかかる力は最大許容力を超えてはならない:
バー![]() は圧縮されている.
は圧縮されている.![]() を材料の圧縮応力とする.
を材料の圧縮応力とする.![]() にかかる力は最大許容力を超えてはならない:
にかかる力は最大許容力を超えてはならない:
幾何最適化問題の特定の例は,![]() の与えられた値について解くことができる.接合部
の与えられた値について解くことができる.接合部 ![]() の垂直位置が特定の範囲内にあると仮定して一連の問題を解く:
の垂直位置が特定の範囲内にあると仮定して一連の問題を解く:
自由端上の垂直重み ![]() に従う,重みが最小の片持ち梁を設計する.この梁は単位長の
に従う,重みが最小の片持ち梁を設計する.この梁は単位長の ![]() 個の部分からなっている.各部分の幅は
個の部分からなっている.各部分の幅は ![]() で高さは
で高さは ![]() である:
である:
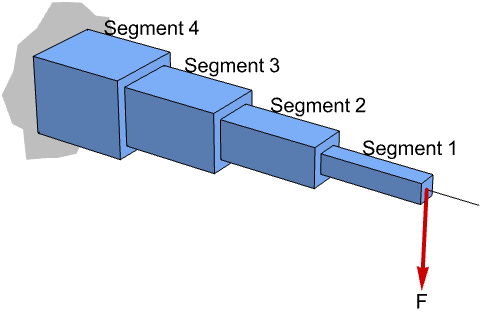
荷重によって梁はたわみ,梁の各部分にストレス ![]() がかかる.このストレスは最大許容応力
がかかる.このストレスは最大許容応力 ![]() より小さくなければならない:
より小さくなければならない:
![]() を部分
を部分 ![]() の右端のたわみとする.自由端のたわみ
の右端のたわみとする.自由端のたわみ ![]() は
は ![]() で再帰的に求められる.
で再帰的に求められる.![]() はヤング率で傾き
はヤング率で傾き ![]() である.部分
である.部分 ![]() は固定されているので
は固定されているので ![]() である:
である:
回路の問題 (3)
デジタル回路ゲートのサイジング.回路内の遅延が最小となるような力と面積の制約条件に従って,指定された回路内のゲートの最適サイズを求める.7ゲート回路について考えてみる:
各ゲートが占める面積はこの倍率に比例すると考えられる.総回路面積は以下のようになる:
ゲート ![]() の遷移によるエネルギー損失は,スケール因子
の遷移によるエネルギー損失は,スケール因子 ![]() ,ゲート
,ゲート ![]() の遷移周波数,ゲート遷移におけるエネルギー損失
の遷移周波数,ゲート遷移におけるエネルギー損失 ![]() に比例する:
に比例する:
ゲート ![]() の入力容量は,ゲート6およびゲート7を除いて
の入力容量は,ゲート6およびゲート7を除いて ![]() である.ゲート6およびゲート7の入力容量は10である:
である.ゲート6およびゲート7の入力容量は10である:
ゲート ![]() の容量は,その出力が接続されているゲート(ただしゲート6とゲート7を除く)の入力容量の合計である.出力ゲート6と7の容量はその入力容量と同じである:
の容量は,その出力が接続されているゲート(ただしゲート6とゲート7を除く)の入力容量の合計である.出力ゲート6と7の容量はその入力容量と同じである:
目的は,回路が横断するあらゆる経路の組合せにおける最悪の遅延を最小にすることである:
消費される電力は指定された最大許容電力未満でなければならない:
最大許容面積と最大許容電力のさまざまな組合せについて最小面積を求める:
容量が既知である回路内の相互接続されたネットワークにおける ![]() 本のワイヤ断片の幅を求める.以下のネットワーク内には5本のワイヤ断片がある:
本のワイヤ断片の幅を求める.以下のネットワーク内には5本のワイヤ断片がある:
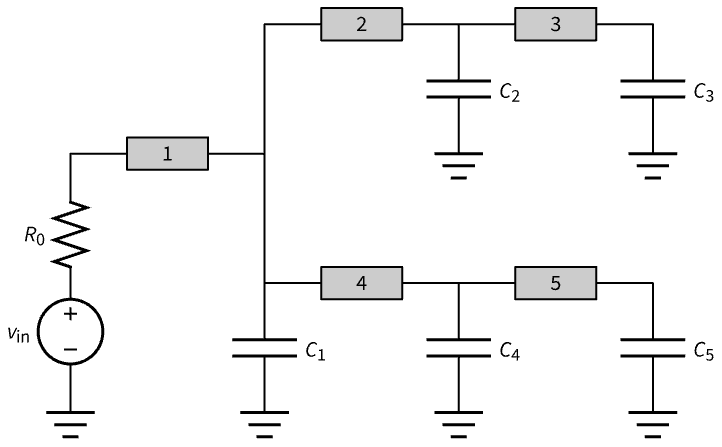
各ワイヤ断片について,抵抗 ![]() ,容量
,容量 ![]() である.
である.![]() はワイヤ特性に依存する正の定数,
はワイヤ特性に依存する正の定数,![]() はワイヤの長さ,幅は
はワイヤの長さ,幅は ![]() である:
である:
![]() モデルを使うと,各ワイヤは抵抗とコンデンサを使ってモデル化できる.結果のネットワークは抵抗・コンデンサネットワークになる:
モデルを使うと,各ワイヤは抵抗とコンデンサを使ってモデル化できる.結果のネットワークは抵抗・コンデンサネットワークになる:
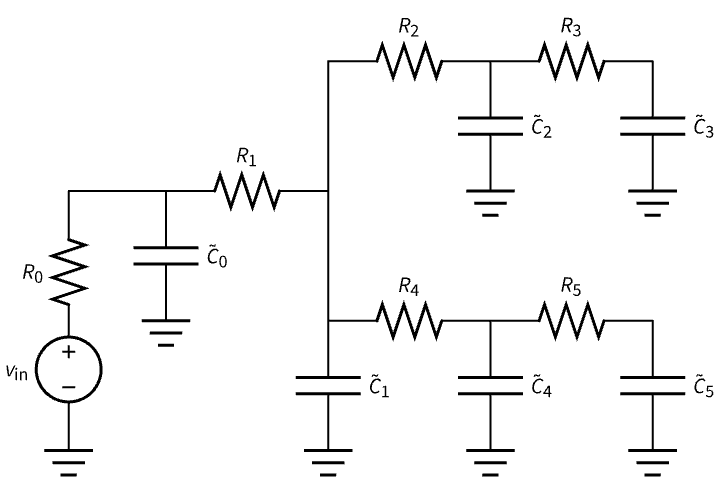
モデルの新たな容量は,個々のネットワークの容量とワイヤ容量 ![]() を合計することで得られる:
を合計することで得られる:
エルモア(Elmore)遅延は電圧変化と新しい値への収束の遅延を測定する.各コンデンサ ![]() のエルモア遅延は
のエルモア遅延は ![]() である.ただし,
である.ただし,![]() はコンデンサ
はコンデンサ ![]() と
と ![]() の間の抵抗の集合である:
の間の抵抗の集合である:
ベースの通過時間が最小化されるようなトランジスタの最適ドーピングプロファイルを求める.ドーピングプロファイルを ![]() とする.ただし,
とする.ただし,![]() はベース幅である.
はベース幅である.![]() をベースの通過時間とする.
をベースの通過時間とする.![]() の関数としての簡約モデルは
の関数としての簡約モデルは ![]() で与えられる.ただし,
で与えられる.ただし,![]() は定数である.
は定数である.![]() とすると,
とすると,![]() 個の等間隔に置かれた点を使って積分を離散化することができる:
個の等間隔に置かれた点を使って積分を離散化することができる:
ドーピングプロファイルには上限と下限があり,初期状態と最終状態が指定されている:
電力制御 (1)
テキスト
Wolfram Research (2020), GeometricOptimization, Wolfram言語関数, https://reference.wolfram.com/language/ref/GeometricOptimization.html.
CMS
Wolfram Language. 2020. "GeometricOptimization." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GeometricOptimization.html.
APA
Wolfram Language. (2020). GeometricOptimization. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GeometricOptimization.html