ConicOptimization[f,cons,vars]
finds values of variables vars that minimize the linear objective f subject to conic constraints cons.
ConicOptimization[…,"prop"]
specifies what solution property "prop" should be returned.






ConicOptimization
ConicOptimization[f,cons,vars]
finds values of variables vars that minimize the linear objective f subject to conic constraints cons.
ConicOptimization[…,"prop"]
specifies what solution property "prop" should be returned.
Details and Options







- Conic optimization is also known as mixed-integer conic optimization, linear conic optimization or linear conic programming.
- Conic optimization includes many other forms of optimization, including linear optimization, linear fractional optimization, quadratic optimization, second-order cone optimization, semidefinite optimization and geometric optimization.
- Conic optimization is a convex optimization problem that can be solved globally and efficiently with real, integer or complex variables.
- Conic optimization finds
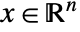 that solves the primal problem:
that solves the primal problem: -
minimize 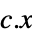
subject to constraints 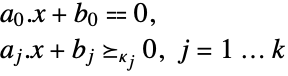
where 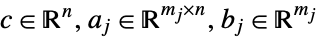
- The set
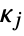 should be a proper convex cone of dimension
should be a proper convex cone of dimension 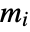 . Common cone specifications for
. Common cone specifications for 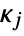 and the sets corresponding to
and the sets corresponding to 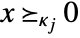 (VectorGreaterEqual[{x,0},κj]) are:
(VectorGreaterEqual[{x,0},κj]) are: -
{"NonNegativeCone", m} 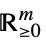
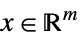 such that
such that 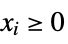
{"NormCone", m} 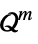
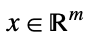 such that
such that ![TemplateBox[{{{, {{x, _, 1}, ,, ..., ,, {x, _, {(, {m, -, 1}, )}}}, }}}, Norm]<=x_m TemplateBox[{{{, {{x, _, 1}, ,, ..., ,, {x, _, {(, {m, -, 1}, )}}}, }}}, Norm]<=x_m](Files/ConicOptimization.en/14.png)
{"SemidefiniteCone", m} 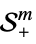
symmetric positive semidefinite matrices 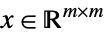
"ExponentialCone" 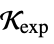
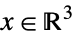 such that
such that 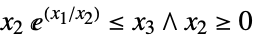
"DualExponentialCone" 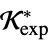
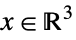 such that
such that 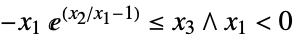 or
or 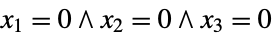
{"PowerCone",α} 
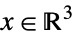 such that
such that 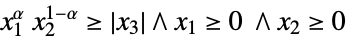
{"DualPowerCone",α} 
 such that
such that 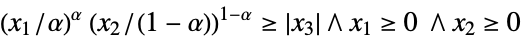
- Mixed-integer conic optimization finds
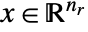 and
and 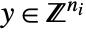 that solve the problem:
that solve the problem: -
minimize 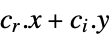
subject to constraints 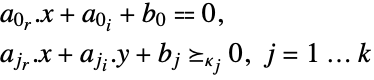
where 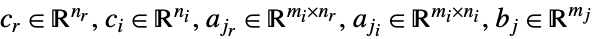
- When the objective function is real valued, ConicOptimization solves problems with
![x in TemplateBox[{}, Complexes]^n x in TemplateBox[{}, Complexes]^n](Files/ConicOptimization.en/35.png) by internally converting to real variables
by internally converting to real variables 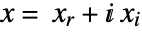 , where
, where 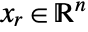 and
and 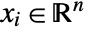 .
. - The variable specification vars should be a list with elements giving variables in one of the following forms:
-
v variable with name 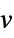 and dimensions inferred
and dimensions inferredv∈Reals real scalar variable v∈Integers integer scalar variable v∈Complexes complex scalar variable v∈ℛ vector variable restricted to the geometric region 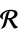
v∈Vectors[n,dom] vector variable in 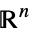 or
or 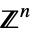
v∈Matrices[{m,n},dom] matrix variable in 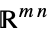 or
or 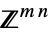
- The constraints cons can be specified by:
-
LessEqual 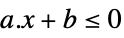
scalar inequality GreaterEqual 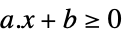
scalar inequality VectorLessEqual 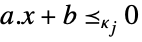
vector inequality VectorGreaterEqual 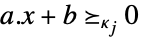
vector inequality Equal 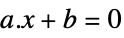
scalar or vector equality Element 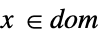
convex domain or region element - With ConicOptimization[f,cons,vars], parameter equations of the form parval, where par is not in vars and val is numerical or an array with numerical values, may be included in the constraints to define parameters used in f or cons. »
- The primal minimization problem has a related maximization problem that is the Lagrangian dual problem. The dual maximum value is always less than or equal to the primal minimum value, so it provides a lower bound. The dual maximizer provides information about the primal problem, including sensitivity of the minimum value to changes in the constraints. »
- The conic optimization has a dual problem: »
-
maximize 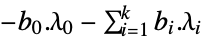
subject to constraints 
where 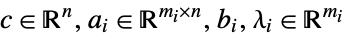 and
and 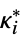 is the dual cone to
is the dual cone to 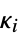
- The possible solution properties "prop" include: »
-
"PrimalMinimizer" 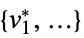
a list of variable values that minimizes 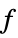
"PrimalMinimizerRules" 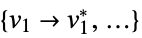
values for the variables vars={v1,…} that minimize 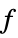
"PrimalMinimizerVector" 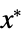
the vector that minimizes 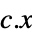
"PrimalMinimumValue" 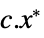
the minimum value 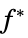
"DualMaximizer" 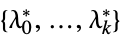
the vector that maximizes 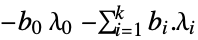
"DualMaximumValue" 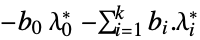
the dual maximum value "DualityGap" 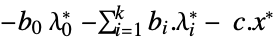
the difference between the dual and primal optimal values "Slack" 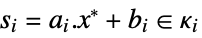
vectors that convert inequality constraints to equality "ConstraintSensitivity" 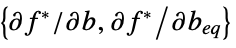
sensitivity of 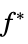 to constraint perturbations
to constraint perturbations"ObjectiveVector" 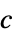
the linear objective vector "ConicConstraints" 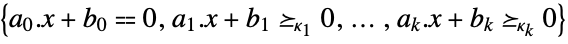
the list of conic constraints in canonical form "ConicConstraintConeSpecifications" 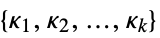
the list of specifications for the cones 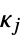
"ConicConstraintConeDimensions" ![{TemplateBox[{Dimensions, paclet:ref/Dimensions}, RefLink, BaseStyle -> {3ColumnTableMod}][kappa_1],...} {TemplateBox[{Dimensions, paclet:ref/Dimensions}, RefLink, BaseStyle -> {3ColumnTableMod}][kappa_1],...}](Files/ConicOptimization.en/75.png)
the list of dimensions for the cones in the conic constraints "ConicConstraintAffineLists" 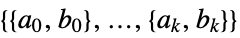
the list of matrix, vector pairs for the affine transforms in the conic constraints {"prop1","prop2",…} several solution properties - The following options may be given:
-
MaxIterations Automatic maximum number of iterations to use Method Automatic the method to use PerformanceGoal $PerformanceGoal aspects of performance to try to optimize Tolerance Automatic the tolerance to use for internal comparisons - The option Method->method may be used to specify the method to use. Available methods include:
-
Automatic choose the method automatically "SCS" SCS splitting conic solver "CSDP" CSDP semidefinite optimization solver "DSDP" DSDP semidefinite optimization solver "MOSEK" commercial MOSEK convex optimization solver "Gurobi" commercial Gurobi linear and quadratic optimization solver "Xpress" commercial Xpress linear and quadratic optimization solver - Computations are limited to MachinePrecision.
Examples
open all close allBasic Examples (3)
Scope (35)
Basic Uses (11)
Minimize ![]() subject to constraints
subject to constraints ![]() :
:
Several linear inequality constraints can be expressed with VectorGreaterEqual:
Use ![]() v>=
v>=![]() or \[VectorGreaterEqual] to enter the vector inequality sign :
or \[VectorGreaterEqual] to enter the vector inequality sign :
An equivalent form using scalar inequalities:
The inequality ![]() may not be the same as
may not be the same as ![]() due to possible threading in
due to possible threading in ![]() :
:
To avoid unintended threading in ![]() , use Inactive[Plus]:
, use Inactive[Plus]:
Use constant parameter equations to avoid unintended threading in ![]() :
:
VectorGreaterEqual represents a conic inequality with respect to the "NonNegativeCone":
To explicitly specify the dimension of the cone, use {"NonNegativeCone",n}:
Minimize ![]() subject to the constraint
subject to the constraint ![]() :
:
Specify the constraint ![]() using a conic inequality with "NormCone":
using a conic inequality with "NormCone":
Minimize ![]() subject to the positive semidefinite matrix constraint
subject to the positive semidefinite matrix constraint ![]() :
:
Use a vector variable ![]() and Indexed[x,i] to specify individual components:
and Indexed[x,i] to specify individual components:
Use Vectors[n] to specify the dimension of a vector variable when it is ambiguous:
Specify non-negative constraints using NonNegativeReals (![]() ):
):
Integer Variables (4)
Specify integer domain constraints using Integers:
Specify integer domain constraints on vector variables using Vectors[n,Integers]:
Specify non-negative integer domain constraints using NonNegativeIntegers (![]() ):
):
Specify non-positive integer domain constraints using NonPositiveIntegers (![]() ):
):
Complex Variables (5)
Specify complex variables using Complexes:
Minimize a real objective ![]() with complex variables and complex constraints
with complex variables and complex constraints ![]() :
:
Let ![]() . Expanding out the constraints into real components gives the following:
. Expanding out the constraints into real components gives the following:
Solve the problem with real-valued objective and complex variables and constraints:
Solve the same problem with real variables and constraints:
Use a quadratic constraint ![]() with a Hermitian matrix
with a Hermitian matrix ![]() and real-valued variables:
and real-valued variables:
Use a Hermitian matrix ![]() in a constraint
in a constraint ![]() with complex variables:
with complex variables:
Use a linear matrix inequality constraint ![]() with Hermitian or real symmetric matrices:
with Hermitian or real symmetric matrices:
The variables in linear matrix inequalities need to be real for the sum to remain Hermitian:
Primal Model Properties (4)
Minimize ![]() over the intersection of a triangle
over the intersection of a triangle ![]() and a disk
and a disk ![]() :
:
Get the primal minimizer as a vector:
Extract the conic constraints:
Extract the cone specification ![]() in the conic constraints:
in the conic constraints:
Extract the cone dimensions ![]() in the conic constraints:
in the conic constraints:
Extract the affine lists ![]() in the conic constraints:
in the conic constraints:
The slack for an inequality ![]() at the minimizer
at the minimizer ![]() is given by
is given by ![]() :
:
Extract the minimizer and conic constraint affine lists:
Verify that the slack satisfies s={s0,…,sk} with aj.x*+bj-sj=0.
A conic optimization problem in standard form is defined by some authors as minimizing ![]() subject to
subject to ![]() and
and ![]() . To convert to standard form, for each conic constraint
. To convert to standard form, for each conic constraint ![]() , add a variable
, add a variable ![]() and corresponding linear equality constraint
and corresponding linear equality constraint ![]() :
:
Extract the objective vector, conic constraint affine lists and the conic specifications:
The slack constraints ![]() are the same as
are the same as ![]() :
:
Form the linear equality constraint ![]() :
:
Solve the transformed standard form conic problem:
The "Slack" property allows you to get the values of ![]() without doing the actual transformation:
without doing the actual transformation:
Dual Model Properties (3)
The dual problem is to maximize ![]() subject to
subject to ![]() :
:
The primal minimum value and the dual maximum value coincide because of strong duality:
That is the same as having a duality gap of zero. In general, ![]() at optimal points:
at optimal points:
Construct the dual problem using coefficients extracted from the primal problem:
Extract the objective vector and constraint affine lists:
The dual problem is to maximize ![]() subject to
subject to ![]() :
:
Get the dual maximum value and dual maximizer directly using solution properties:
The "DualMaximizer" can be obtained with:
The dual maximizer vector partitions match the number and dimensions of the dual cones:
Sensitivity Properties (3)
Find the change in optimal value due to constraint perturbations:
Compute the "ConstraintSensitivity":
Consider new constraint ![]() where
where ![]() is the perturbation:
is the perturbation:
The new optimal value can be estimated to be:
Compare to directly solving the perturbed problem:
The optimal value changes according to the signs of the sensitivity elements:
At negative sensitivity element position, a positive perturbation will decrease the optimal value:
At positive sensitivity element position, a positive perturbation will increase the optimal value:
The constraint sensitivity can also be obtained as the negative of the dual maximizer:
Supported Convex Cones (5)
"NonNegativeCone" (1)
"NormCone" (1)
"SemidefiniteCone" (1)
"ExponentialCone" (1)
Options (11)
Method (8)
"SCS" uses a splitting conic solver method:
"CSDP" is an interior point method for semidefinite problems:
"DSDP" is an alternative interior point method for semidefinite problems:
"IPOPT" is an interior point method for nonlinear problems:
Different methods have different default tolerances, which affects the accuracy and precision:
Compute exact and approximate solutions:
"SCS" has a default tolerance of ![]() :
:
"CSDP", "DSDP" and "IPOPT" have default tolerances of ![]() :
:
When method "SCS" is specified, it is called with the SCS library default tolerance of 10-3:
With default options, this problem is solved by method "SCS" with tolerance 10-6:
Use methods "CSDP" or "DSDP" for up to semidefinite constraints:
Solve the problem using method "CSDP":
Solve the problem using method "DSDP":
Use method "IPOPT" to obtain accurate solutions when "CSDP" and "DSDP" are not applicable:
"IPOPT" produces more accurate results than "SCS" but is typically slower:
PerformanceGoal (1)
The default value of the option PerformanceGoal is $PerformanceGoal:
Use PerformanceGoal"Quality" to get a more accurate result:
Use PerformanceGoal"Speed" to get a result faster, but at the cost of quality:
Tolerance (2)
A smaller Tolerance setting gives a more precise result:
Compute the exact minimum value with Minimize:
Compute the error in the minimum value with different Tolerance settings:
Visualize the change in minimum value error with respect to tolerance:
A smaller Tolerance setting gives a more precise answer, but may take longer to compute:
Applications (29)
Basic Modeling Transformations (13)
Maximize ![]() subject to
subject to ![]() . Solve a maximization problem by negating the objective function:
. Solve a maximization problem by negating the objective function:
Negate the primal minimum value to get the corresponding maximal value:
Minimize ![]() over a disk centered at
over a disk centered at ![]() with radius
with radius ![]() . Convert the objective
. Convert the objective ![]() into a linear function
into a linear function ![]() with the additional constraint
with the additional constraint ![]() , which is equivalent to
, which is equivalent to ![]() :
:
The disk constraint can also be represented using Norm:
Minimize ![]() over a regular pentagon. Convert the objective into a linear function using
over a regular pentagon. Convert the objective into a linear function using ![]() and the additional constraints
and the additional constraints ![]() :
:
Minimize ![]() . Using auxiliary variable
. Using auxiliary variable ![]() , the objective is transformed to minimize
, the objective is transformed to minimize ![]() subject to the constraint
subject to the constraint ![]() :
:
Minimize ![]() subject to
subject to ![]() . Using two auxiliary variables
. Using two auxiliary variables ![]() , transform the problem to minimize
, transform the problem to minimize ![]() subject to
subject to ![]() :
:
Minimize ![]() . Using auxiliary variable
. Using auxiliary variable ![]() , convert the problem to minimize
, convert the problem to minimize ![]() subject to the constraints
subject to the constraints ![]() :
:
Minimize ![]() subject to
subject to ![]() , where
, where ![]() is a nondecreasing function, by instead minimizing
is a nondecreasing function, by instead minimizing ![]() . The primal minimizer
. The primal minimizer ![]() will remain the same for both problems. Consider minimizing
will remain the same for both problems. Consider minimizing ![]() subject to
subject to ![]() :
:
The true minimum value can be obtained by applying ![]() to the minimum value of
to the minimum value of ![]() :
:
Minimize ![]() over a disk centered at
over a disk centered at ![]() with radius
with radius ![]() Using the auxiliary variable
Using the auxiliary variable ![]() , the objective is transformed to minimizing
, the objective is transformed to minimizing ![]() with the additional constraint
with the additional constraint ![]() :
:
The constraint![]() is equivalent to the exponential cone constraint
is equivalent to the exponential cone constraint ![]() iff
iff ![]() :
:
Minimize ![]() over a disk centered at
over a disk centered at ![]() with radius
with radius ![]() . Using auxiliary variable
. Using auxiliary variable ![]() , convert the problem to minimize
, convert the problem to minimize ![]() subject to the constraint
subject to the constraint ![]() :
:
The constraint ![]() is equivalent to
is equivalent to ![]() . This can be represented using "PowerCone" by
. This can be represented using "PowerCone" by ![]() :
:
Using auxiliary variable ![]() , convert the problem to minimize
, convert the problem to minimize ![]() subject to the constraint
subject to the constraint ![]() :
:
This can be represented using "PowerCone" constraints. Since ![]() iff
iff ![]() , bounding
, bounding ![]() with
with ![]() where
where ![]() gives
gives ![]() :
:
Find ![]() that minimizes the largest eigenvalue of a symmetric matrix that depends linearly on the decision variables
that minimizes the largest eigenvalue of a symmetric matrix that depends linearly on the decision variables ![]() ,
, ![]() . The problem can be formulated as linear matrix inequality since
. The problem can be formulated as linear matrix inequality since ![]() is equivalent to
is equivalent to ![]() , where
, where ![]() is the
is the ![]()
![]() eigenvalue of
eigenvalue of ![]() . Define the linear matrix function
. Define the linear matrix function ![]() :
:
A real symmetric matrix ![]() can be diagonalized with an orthogonal matrix
can be diagonalized with an orthogonal matrix ![]() so
so ![]() . Hence
. Hence ![]() iff
iff ![]() . Since any
. Since any ![]() , taking
, taking ![]() ,
, ![]() , hence
, hence ![]() iff
iff ![]() . Numerically simulate to show that these formulations are equivalent:
. Numerically simulate to show that these formulations are equivalent:
Run a Monte Carlo simulation to check the plausibility of the result:
Minimize ![]() subject to
subject to ![]() , assuming
, assuming ![]() when
when ![]() . Using the auxiliary variable
. Using the auxiliary variable ![]() , the objective is to minimize
, the objective is to minimize ![]() such that
such that ![]() :
:
A Schur complement condition says that if ![]() , a block matrix
, a block matrix ![]() iff
iff ![]() . Therefore
. Therefore ![]() iff
iff ![]() . Use Inactive Plus for constructing the constraints to avoid threading:
. Use Inactive Plus for constructing the constraints to avoid threading:
For quadratic sets ![]() , which include ellipsoids, quadratic cones and paraboloids, determine whether
, which include ellipsoids, quadratic cones and paraboloids, determine whether ![]() , where
, where ![]() are symmetric matrices,
are symmetric matrices, ![]() are vectors and
are vectors and ![]() scalars:
scalars:
Assuming that the sets i are full dimensional, the S-procedure says that ![]() iff there exists some non-negative number
iff there exists some non-negative number ![]() such that
such that ![]() Visually see that there exists a non-negative
Visually see that there exists a non-negative ![]() :
:
Data-Fitting Problems (5)
Minimize ![]() subject to the constraints
subject to the constraints ![]() :
:
Using auxiliary variable ![]() , the transformed objective is to minimize
, the transformed objective is to minimize ![]() subject to
subject to ![]() :
:
Fit a cubic curve to discrete data such that the first and last points of the data lie on the curve:
Construct the matrix using DesignMatrix:
Define the constraint so that the first and last points must lie on the curve:
Find the coefficients ![]() by minimizing
by minimizing ![]() . Using auxiliary variable
. Using auxiliary variable ![]() , the transformed objective is to minimize
, the transformed objective is to minimize ![]() subject to
subject to ![]() :
:
Find a robust fit to nonlinear discrete data by minimizing ![]() :
:
Fit the data using the bases ![]() . The interpolating function will be
. The interpolating function will be ![]() :
:
Since ![]() , using auxiliary variables
, using auxiliary variables ![]() . The problem is transformed to minimize
. The problem is transformed to minimize ![]() subject to the constraints
subject to the constraints ![]() :
:
Compare interpolating function with reference function:
Represent a given polynomial ![]() in terms of sum-of-squares polynomial
in terms of sum-of-squares polynomial ![]() :
:
The objective is to find ![]() such that
such that ![]() , where
, where ![]() is a vector of monomials:
is a vector of monomials:
Construct the symmetric matrix ![]() :
:
Find the polynomial coefficients of ![]() and
and ![]() and make sure they are equal:
and make sure they are equal:
The quadratic term ![]() , where
, where ![]() is a lower-triangular matrix obtained from the Cholesky decomposition of
is a lower-triangular matrix obtained from the Cholesky decomposition of ![]() :
:
Compare the sum-of-squares polynomial to the given polynomial:
Find an ![]() regularized fit to complex data by minimizing
regularized fit to complex data by minimizing ![]() for a complex
for a complex ![]() :
:
Construct the matrix ![]() using DesignMatrix, for the basis
using DesignMatrix, for the basis ![]() :
:
Let ![]() be the fit defined as a function of the real and imaginary components of
be the fit defined as a function of the real and imaginary components of ![]() :
:
Geometry Problems (5)
Find the minimum distance between two disks of radius 1 centered at ![]() and
and ![]() . Let
. Let ![]() be a point on disk 1. Let
be a point on disk 1. Let ![]() be a point on disk 2. The objective is to minimize
be a point on disk 2. The objective is to minimize ![]() . Using auxiliary variable
. Using auxiliary variable ![]() , the transformed objective is to minimize
, the transformed objective is to minimize ![]() subject to
subject to ![]() :
:
Visualize the position of the two points:
The auxiliary variable ![]() gives the distance between the points:
gives the distance between the points:
Find the radius ![]() and center
and center ![]() of a minimal enclosing ball that encompasses a given region:
of a minimal enclosing ball that encompasses a given region:
Minimize the radius ![]() subject to the constraints
subject to the constraints ![]() :
:
The minimal enclosing ball can be found efficiently using BoundingRegion:
Find the plane that separates two non-intersecting convex polygons:
Let ![]() be a point on
be a point on ![]() . Let
. Let ![]() be a point on
be a point on ![]() . The objective is to minimize
. The objective is to minimize ![]() . Using auxiliary variable
. Using auxiliary variable ![]() , the transformed objective is to minimize
, the transformed objective is to minimize ![]() subject to
subject to ![]() :
:
According to the separating hyperplane theorem, the dual associated with the constraint ![]() will give the normal of the hyperplane:
will give the normal of the hyperplane:
The dual associated with the "NormCone" is:
The hyperplane is constructed as:
Visualize the plane separating the two polygons:
Find the maximum area ellipse parametrized as ![]() that can be fitted into a convex polygon:
that can be fitted into a convex polygon:
Each segment of the convex polygon can be represented as intersections of half-planes ![]() . Extract the linear inequalities:
. Extract the linear inequalities:
Applying the parametrization to the half-planes gives ![]() . The term
. The term ![]() . Thus, the constraints are
. Thus, the constraints are![]() :
:
Minimizing the area is equivalent to minimizing ![]() , which is equivalent to minimizing
, which is equivalent to minimizing ![]() :
:
Convert the parameterized ellipse into the explicit form as ![]() :
:
Find the analytic center of a convex polygon. The analytic center is a point that maximizes the product of distances to the constraints:
Each segment of the convex polygon can be represented as intersections of half-planes ![]() . Extract the linear inequalities:
. Extract the linear inequalities:
The objective is to maximize ![]() . Taking
. Taking ![]() and negating the objective, the transformed objective is
and negating the objective, the transformed objective is ![]() :
:
Using auxiliary variable ![]() , the transformed objective is
, the transformed objective is ![]() subject to the constraint
subject to the constraint ![]() :
:
Classification Problems (3)
Find a line ![]() that separates two groups of points
that separates two groups of points ![]() and
and ![]() :
:
For separation, set 1 must satisfy ![]() and set 2 must satisfy
and set 2 must satisfy ![]() :
:
The objective is to minimize ![]() , which gives twice the thickness between
, which gives twice the thickness between ![]() and
and ![]() . Using the auxiliary variable
. Using the auxiliary variable ![]() , the objective function is transformed to the constraint
, the objective function is transformed to the constraint ![]() :
:
Find a quadratic polynomial that separates two groups of 3D points ![]() and
and ![]() :
:
Construct the quadratic polynomial data matrices for the two sets using DesignMatrix:
For separation, set 1 must satisfy ![]() and set 2 must satisfy
and set 2 must satisfy ![]() :
:
Find the separating polynomial by minimizing ![]() . Using auxiliary variable
. Using auxiliary variable ![]() , the transformed objective is to minimize
, the transformed objective is to minimize ![]() with the additional constraint
with the additional constraint ![]() :
:
The polynomial separating the two groups of points is:
Plot the polynomial separating the two datasets:
Separate a given set of points ![]() into different groups. This is done by finding the centers
into different groups. This is done by finding the centers ![]() for each group by minimizing
for each group by minimizing ![]() , where
, where ![]() is a given local kernel and
is a given local kernel and ![]() is a given penalty parameter:
is a given penalty parameter:
The kernel ![]() is a
is a ![]() -nearest neighbor (
-nearest neighbor (![]() ) function such that
) function such that ![]() , else
, else ![]() . For this problem,
. For this problem, ![]() nearest neighbors are selected:
nearest neighbors are selected:
Using the auxiliary variable ![]() , the objective is transformed to minimize
, the objective is transformed to minimize ![]() subject to the constraint
subject to the constraint ![]() :
:
For each data point there exists a corresponding center. Data belonging to the same group will have the same center value:
Optimal Control Problems (1)
The minimizing function integral can be approximated using the trapezoidal rule. The discretized objective function will be ![]() subject to additional constraints
subject to additional constraints ![]() :
:
The time derivative in ![]() is discretized using finite differences:
is discretized using finite differences:
The initial condition constraints ![]() can be specified using Indexed:
can be specified using Indexed:
Using auxiliary variable ![]() , the objective is transformed to minimize
, the objective is transformed to minimize ![]() subject to
subject to ![]() :
:
Convert the discretized result into InterpolatingFunction:
Plot the state variables. The state variables try and track the function ![]() :
:
Facility Location Problems (1)
Find the positions of various cell towers ![]() and the range
and the range ![]() needed to serve clients located at
needed to serve clients located at ![]() :
:
Each cell tower consumes power proportional to its range, which is given by ![]() . The objective is to minimize the power consumption:
. The objective is to minimize the power consumption:
Let ![]() be a decision variable indicating that
be a decision variable indicating that ![]() if client
if client ![]() is covered by cell tower
is covered by cell tower ![]() :
:
Each cell tower must be located such that its range covers some of the clients:
Each cell tower can cover multiple clients:
Each cell tower has a minimum and maximum coverage:
Find the cell tower positions and their ranges:
Extract cell tower position and range:
Visualize the position and range of the towers with respect to client locations:
Portfolio Optimization (1)
Find the distribution of capital ![]() to invest in six stocks to maximize return while minimizing risk:
to invest in six stocks to maximize return while minimizing risk:
The return is given by ![]() , where
, where ![]() is a vector of expected return value of each individual stock:
is a vector of expected return value of each individual stock:
The risk is given by ![]() ;
; ![]() is a risk-aversion parameter and
is a risk-aversion parameter and ![]() :
:
The objective is to maximize return while minimizing risk for a specified risk-aversion parameter:
The effect on market prices of stocks due to the buying and selling of stocks is modeled by ![]() , which is modeled by a power cone using the epigraph transformation:
, which is modeled by a power cone using the epigraph transformation:
The weights ![]() must all be greater than 0 and the weights plus market impact costs must add to 1:
must all be greater than 0 and the weights plus market impact costs must add to 1:
Compute the returns and corresponding risk for a range of risk-aversion parameters:
The optimal ![]() over a range of
over a range of ![]() gives an upper-bound envelope on the tradeoff between return and risk:
gives an upper-bound envelope on the tradeoff between return and risk:
Compute the weights for a specified number of risk-aversion parameters:
By accounting for the market costs, a diversified portfolio can be obtained for low risk aversion, but when the risk aversion is high, the market impact cost dominates, due to purchasing a less diversified stock:
Properties & Relations (8)
ConicOptimization gives the global minimum of the objective function:
Plot the objective function with the minimum value over the feasible region:
Minimize gives global exact results for conic problems:
NMinimize can be used to obtain approximate results using global methods:
FindMinimum can be used to obtain approximate results using local methods:
SemidefiniteOptimization is a special case of ConicOptimization:
SecondOrderConeOptimization is a special case of ConicOptimization:
QuadraticOptimization is a special case of ConicOptimization:
Use auxiliary variable ![]() and minimize
and minimize ![]() with additional constraint
with additional constraint ![]() :
:
LinearOptimization is a special case of ConicOptimization:
Possible Issues (6)
The constraints at the optimal point are expected to be satisfied up to some tolerance:
The constraint violation can often be controlled with the Tolerance option:
The minimum value of an empty set or infeasible problem is defined to be ![]() :
:
The minimizer is Indeterminate:
The minimum value for an unbounded set or unbounded problem is ![]() :
:
The minimizer is Indeterminate:
Badly scaled problems can produce results with large error:
After scaling ![]() by 10-10, this is mathematically equivalent to the following problem:
by 10-10, this is mathematically equivalent to the following problem:
Any result for ![]() ,
, ![]() within ±10-6 of 5*10-10 will fall within the tolerance of 10-6 and when scaled back can produce an error of up to:
within ±10-6 of 5*10-10 will fall within the tolerance of 10-6 and when scaled back can produce an error of up to:
You could solve the preceding scaled problem or try to tighten the default tolerance:
Dual related solution properties for mixed-integer problems may not be available:
Constraints with complex values need to be specified using vector inequalities:
Just using Less will not work even when both sides are real in theory:
Tech Notes
Related Guides
Text
Wolfram Research (2019), ConicOptimization, Wolfram Language function, https://reference.wolfram.com/language/ref/ConicOptimization.html (updated 2020).
CMS
Wolfram Language. 2019. "ConicOptimization." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/ConicOptimization.html.
APA
Wolfram Language. (2019). ConicOptimization. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ConicOptimization.html
BibTeX
@misc{reference.wolfram_2025_conicoptimization, author="Wolfram Research", title="{ConicOptimization}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/ConicOptimization.html}", note=[Accessed: 06-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_conicoptimization, organization={Wolfram Research}, title={ConicOptimization}, year={2020}, url={https://reference.wolfram.com/language/ref/ConicOptimization.html}, note=[Accessed: 06-February-2026]}