DesignMatrix

DesignMatrix[{{x11,x12,…,y1},{x21,x22,…,y2},…},{f1,f2,…},{x1,x2,…}]

constructs the design matrix for the linear model β0+β1 f1+β2 f2+….

Details and Options

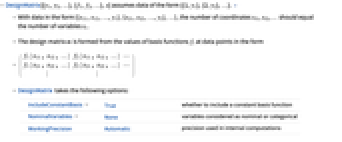
  • DesignMatrix[{y1,y2,…},{f1,f2,…},x] assumes data of the form {{1,y1},{2,y2},…}. »
  • With data in the form 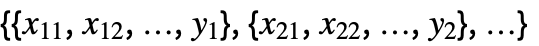{{x_(11),x_(12),...,y_(1)},{x_(21),x_(22),...,y_(2)},...}, the number of coordinates xi1, xi2, … should equal the number of variables xi.
  • The design matrix m is formed from the values of basis functions fi at data points in the form
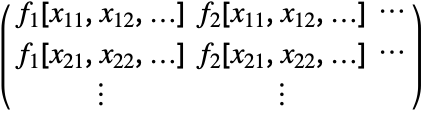
  • DesignMatrix takes the following options:
  • IncludeConstantBasis Truewhether to include a constant basis function
    NominalVariables Nonevariables considered as nominal or categorical
    WorkingPrecisionAutomaticprecision used in internal computations
  • With the setting IncludeConstantBasis->False, the design matrix for a model of form β1 f1+β2 f2+⋯ is constructed. »

Examples

open allclose all

Basic Examples  (3)

Design matrix for a linear model:

Add a quadratic term:

Leave out the constant term:

Design matrix with two predictor variables:

Include a product term:

Assume predictor values 1, 2, …:

Scope  (2)

Use any numeric functions of the predictors:

Get the design matrix using exact arithmetic:

Use machine arithmetic:

Use arbitrary-precision arithmetic:

Use fixed 24-digit precision arithmetic:

Options  (3)

IncludeConstantBasis  (1)

A constant term is included by default:

Construct a design matrix without a constant term:

NominalVariables  (2)

Treat x as a numeric variable:

Treat x as nominal:

Use nominal variables that are not numeric:

Treat only x as nominal:

Treat all predictors as nominal:

Properties & Relations  (1)

DesignMatrix constructs the design matrix used by LinearModelFit:

The matrix is the same for GeneralizedLinearModelFit:

Wolfram Research (2008), DesignMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/DesignMatrix.html.

Text

Wolfram Research (2008), DesignMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/DesignMatrix.html.

CMS

Wolfram Language. 2008. "DesignMatrix." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DesignMatrix.html.

APA

Wolfram Language. (2008). DesignMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DesignMatrix.html

BibTeX

@misc{reference.wolfram_2024_designmatrix, author="Wolfram Research", title="{DesignMatrix}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/DesignMatrix.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_designmatrix, organization={Wolfram Research}, title={DesignMatrix}, year={2008}, url={https://reference.wolfram.com/language/ref/DesignMatrix.html}, note=[Accessed: 21-November-2024 ]}