LinearFractionalOptimization[f,cons,vars]
finds values of variables vars that minimize the linear fractional objective f subject to linear constraints cons.
LinearFractionalOptimization[{α,β,γ,δ},{a,b}]
finds a vector ![]() that minimizes the linear fractional function
that minimizes the linear fractional function ![]() subject to the linear inequality constraints
subject to the linear inequality constraints ![]() .
.
LinearFractionalOptimization[{α,β,γ,δ},{a,b},{aeq,beq}]
includes the linear equality constraints ![]() .
.
LinearFractionalOptimization[{α,β,γ,δ},…,{dom1,dom2,…}]
takes ![]() to be in the domain domi, where domi is Integers or Reals.
to be in the domain domi, where domi is Integers or Reals.
LinearFractionalOptimization[…,"prop"]
specifies what solution property "prop" should be returned.




LinearFractionalOptimization
LinearFractionalOptimization[f,cons,vars]
finds values of variables vars that minimize the linear fractional objective f subject to linear constraints cons.
LinearFractionalOptimization[{α,β,γ,δ},{a,b}]
finds a vector ![]() that minimizes the linear fractional function
that minimizes the linear fractional function ![]() subject to the linear inequality constraints
subject to the linear inequality constraints ![]() .
.
LinearFractionalOptimization[{α,β,γ,δ},{a,b},{aeq,beq}]
includes the linear equality constraints ![]() .
.
LinearFractionalOptimization[{α,β,γ,δ},…,{dom1,dom2,…}]
takes ![]() to be in the domain domi, where domi is Integers or Reals.
to be in the domain domi, where domi is Integers or Reals.
LinearFractionalOptimization[…,"prop"]
specifies what solution property "prop" should be returned.
Details and Options







- Linear fractional optimization is also known as linear fractional programming (LFP) and mixed-integer fractional linear programming (MILFP).
- Linear fractional optimization is a convex optimization problem that can be solved globally and efficiently with real, integer or complex variables.
- Linear fractional optimization finds
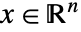 that solves the primal problem: »
that solves the primal problem: » -
minimize 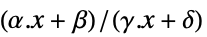
subject to constraints 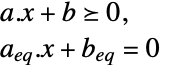
where 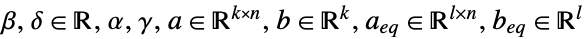
- Mixed-integer linear fractional optimization finds
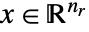 and
and 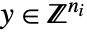 that solve the problem:
that solve the problem: -
minimize 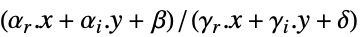
subject to constraints 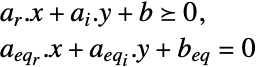
where 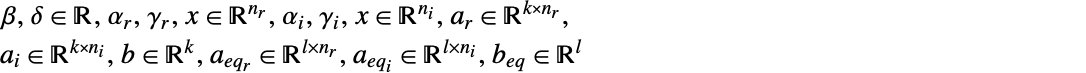
- When the objective function is real valued, LinearFractionalOptimization solves problems with
![x in TemplateBox[{}, Complexes]^n x in TemplateBox[{}, Complexes]^n](Files/LinearFractionalOptimization.en/15.png) by internally converting to real variables
by internally converting to real variables 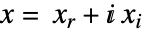 , where
, where 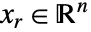 and
and 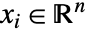 .
. - The variable specification vars should be a list with elements giving variables in one of the following forms:
-
v variable with name 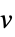 and dimensions inferred
and dimensions inferredv∈Reals real scalar variable v∈Integers integer scalar variable v∈Complexes complex scalar variable v∈ℛ vector variable restricted to the geometric region 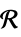
v∈Vectors[n,dom] vector variable in 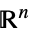 or
or 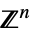
v∈Matrices[{m,n},dom] matrix variable in 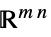 or
or 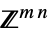
- The constraints cons can be specified by:
-
LessEqual 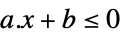
scalar inequality GreaterEqual 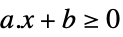
scalar inequality VectorLessEqual 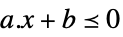
vector inequality VectorGreaterEqual 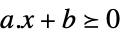
vector inequality Equal 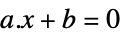
scalar or vector equality Element 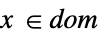
convex domain or region element - With LinearFractionalOptimization[f,cons,vars], parameter equations of the form parval, where par is not in vars and val is numerical or an array with numerical values, may be included in the constraints to define parameters used in f or cons.
- The primal minimization problem has a related maximization problem that is the Lagrangian dual problem. The dual maximum value is always less than or equal to the primal minimum value, so it provides a lower bound. The dual maximizer provides information about the primal problem, including sensitivity of the minimum value to changes in the constraints.
- The Lagrangian dual problem for linear fractional optimization is given by: »
-
maximize 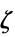
subject to constraints 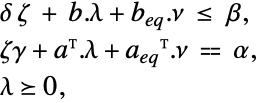
where 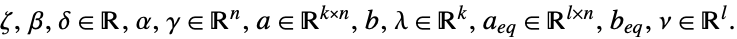
- For linear fractional optimization, strong duality always holds, meaning that if there is a solution to the primal minimization problem, then there is a solution to the dual maximization problem, and the dual maximum value is equal to the primal minimum value.
- The possible solution properties "prop" include:
-
"PrimalMinimizer" 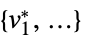
a list of variable values that minimize the objective function "PrimalMinimizerRules" 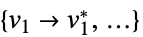
values for the variables vars={v1,…} that minimize 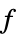
"PrimalMinimizerVector" 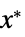
the vector that minimizes 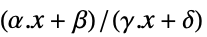
"PrimalMinimumValue" 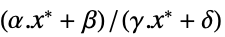
the minimum value 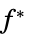
"DualMaximizer" 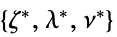
the vectors that maximize 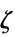
"DualMaximumValue" 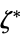
the dual maximum value "DualityGap" 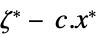
the difference between the dual and primal optimal values (0 because of strong duality) "Slack" 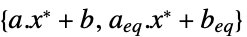
- the constraint slack vector
"ConstraintSensitivity" 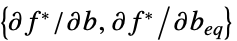
sensitivity of 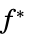 to constraint perturbations
to constraint perturbations"LinearFractionalObjectiveCoefficients" 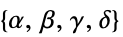
the coefficients in 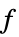
"LinearInequalityConstraints" 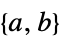
the linear inequality constraint matrix and vector "LinearEqualityConstraints" 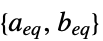
the linear equality constraint matrix and vector {"prop1","prop2",…} several solution properties - The dual maximum value
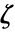 is related to
is related to 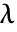 and
and 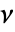 through
through 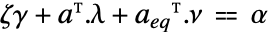 .
. - The following options may be given:
-
MaxIterations Automatic maximum number of iterations to use Method Automatic the method to use PerformanceGoal $PerformanceGoal aspects of performance to try to optimize Tolerance Automatic the tolerance to use for internal comparisons WorkingPrecision Automatic precision to use in internal computations - The option Method->method may be used to specify the method to use. Available methods include:
-
Automatic choose the method automatically "Simplex" simplex method "RevisedSimplex" revised simplex method "InteriorPoint" interior point method (machine precision only) "CLP" COIN library linear programming (machine precision only) "MOSEK" commercial MOSEK linear optimization solver "Gurobi" commercial Gurobi linear optimization solver "Xpress" commercial Xpress linear optimization solver - With WorkingPrecision->Automatic, the precision is taken automatically from the precision of the input arguments unless a method is specified that only works with machine precision, in which case machine precision is used.
- If it is a priori known that the solution sought is where the denominator is either positive or negative, then including a constraint in a and b equivalent to positivity or negativity of the denominator will allow LinearFractionalOptimization to compute the solution more quickly.
Examples
open all close allBasic Examples (3)
Scope (33)
Basic Uses (17)
Minimize ![]() subject to the constraints
subject to the constraints ![]() and
and ![]() :
:
Minimize ![]() subject to the constraints
subject to the constraints ![]() and
and ![]() :
:
Minimize ![]() subject to
subject to ![]() and bounds
and bounds ![]() :
:
Use VectorLessEqual to express several LessEqual inequality constraints at once:
Use ![]() v<=
v<=![]() to enter the vector inequality in a compact form:
to enter the vector inequality in a compact form:
An equivalent form using scalar inequalities:
Use VectorGreaterEqual to express several GreaterEqual inequality constraints at once:
Use ![]() v>=
v>=![]() to enter the vector inequality in a compact form:
to enter the vector inequality in a compact form:
An equivalent form using scalar inequalities:
Use Equal to express several equality constraints at once:
An equivalent form using several scalar equalities:
Specify constraints using a combination of scalar and vector inequalities:
Minimize ![]() subject to
subject to ![]() . Use vector variable
. Use vector variable ![]() :
:
An equivalent form using scalar variables:
Use vector variables and vector inequalities to specify the problem:
Use Indexed to access components of a vector variable, e.g. ![]() :
:
Use constant parameter equations to specify the coefficients of the objective and constraints:
Use constant parameter equations to specify coefficients of several constraints:
Use Vectors[n] to specify the dimension of vector variables when needed:
Specify non-negative constraints using NonNegativeReals (![]() ):
):
An equivalent form using vector inequalities:
Specify non-positive constraints using NonPositiveReals (![]() ):
):
An equivalent form using vector inequalities:
Minimize ![]() subject to
subject to ![]() by specifying the scalars, vectors and matrices:
by specifying the scalars, vectors and matrices:
Solve using the matrix-vector form:
The equivalent form using variables and inequalities:
Try to find a vector ![]() that minimizes the function
that minimizes the function ![]() subject to the constraints
subject to the constraints ![]() :
:
The minimum value is unbounded because there is a singularity across the feasible region:
Integer Variables (4)
Specify integer domain constraints using Integers:
Specify integer domain constraints on vector variables using Vectors[n,Integers]:
Specify non-negative integer domain constraints using NonNegativeIntegers (![]() ):
):
An equivalent form using vector inequalities:
Specify non-positive integer domain constraints using NonPositiveIntegers (![]() ):
):
Complex Variables (2)
Primal Model Properties (3)
Get the primal minimizer as a vector:
Solve an optimization problem using symbolic inputs:
Extract the matrix-vector inputs of the optimization problem:
Recover the symbolic input result using the matrix-vector inputs:
Find the slack associated with a minimization problem:
Get the primal minimizer and the constraint matrices:
The slack for inequality constraints ![]() is a vector
is a vector ![]() such that
such that ![]() :
:
The slack for the equality constraints ![]() is a vector
is a vector ![]() such that
such that ![]() :
:
Dual Model Properties (3)
The dual problem is to maximize ![]() subject to
subject to ![]() :
:
The primal minimum value and the dual maximum value coincide because of strong duality:
The duality gap of zero. In general, ![]() at optimal points:
at optimal points:
Construct the dual problem using constraint matrices extracted from the primal problem:
Extract the objective vectors and constraint matrices:
The dual problem is to maximize ![]() subject to
subject to ![]() . Use Inactive[Times] to avoid threading in equality constraint:
. Use Inactive[Times] to avoid threading in equality constraint:
Get the dual maximum value directly using solution properties:
Sensitivity Properties (4)
Use "ConstraintSensitivity" to find the change in optimal value due to constraint relaxations:
The first vector is inequality sensitivity and the second is equality sensitivity:
Consider new constraints ![]() where
where ![]() is the relaxation. The approximate new optimal value is:
is the relaxation. The approximate new optimal value is:
Compare directly by solving the relaxed problem:
Each sensitivity is associated with inequality or equality constraints:
The inequality constraints and their associated sensitivity:
The equality constraints and their associated sensitivity:
The change in optimal value due to constraint relaxation is proportional to the sensitivity value:
Compute the minimal value and constraint sensitivity:
A zero sensitivity will not change the optimal value if the constraint is relaxed:
A negative sensitivity will decrease the optimal value:
A positive sensitivity will increase the optimal value:
The "ConstraintSensitivity" is related to the dual maximizer of the problem:
The inequality sensitivity ![]() satisfies
satisfies ![]() , where
, where ![]() is the dual inequality maximizer:
is the dual inequality maximizer:
The equality sensitivity ![]() satisfies
satisfies ![]() , where
, where ![]() is the dual equality maximizer:
is the dual equality maximizer:
Options (8)
Method (4)
The default method for MachinePrecision is "CLP":
The default method for arbitrary or infinite WorkingPrecision is "Simplex":
All methods work for MachinePrecision input:
"Simplex" and "RevisedSimplex" can be used for arbitrary- and infinite-precision inputs:
Different methods have different strengths, which is typically problem and implementation dependent:
"Simplex" and "RevisedSimplex" are good for small dense problems:
"InteriorPoint" and "CLP" are good for large sparse problems:
Different methods may give different results for problems where the optimal solution set is not unique:
"InteriorPoint" may return a solution in the middle of the optimal solution set:
"Simplex" always returns a solution at a corner of the optimal solution set:
Tolerance (2)
A smaller Tolerance setting gives a more precise result:
Compute minimum value with very small tolerance to serve as reference:
Compute the solution using different Tolerance settings:
Visualize the change in error with respect to tolerance:
A smaller Tolerance setting gives a more precise answer but typically takes longer to compute:
WorkingPrecision (2)
Exact input gives exact output:
Use MachinePrecision to get an inexact result:
LinearFractionalOptimization can compute results using a higher working precision:
If the precision is less than the precision of the input arguments, a message is issued:
Applications (16)
Basic Modeling Transformations (6)
Maximize ![]() subject to
subject to ![]() . Solve a maximization problem by negating the objective function:
. Solve a maximization problem by negating the objective function:
Negate the primal minimal value to get the corresponding maximum value:
Minimize ![]() subject to
subject to ![]() . Let
. Let ![]() , and convert
, and convert![]() into a linear function using
into a linear function using ![]() :
:
The problem can also be converted using ![]() :
:
Minimize ![]() subject to
subject to ![]() . Since
. Since ![]() , letting
, letting ![]() , the objective is transformed to
, the objective is transformed to ![]() :
:
Minimize ![]() subject to
subject to ![]() . Since
. Since ![]() , using
, using ![]() ,
, ![]() , the objective is transformed to
, the objective is transformed to ![]() :
:
Minimize ![]() subject to
subject to ![]() , where
, where ![]() is a nondecreasing function, by instead minimizing
is a nondecreasing function, by instead minimizing ![]() . The primal minimizer
. The primal minimizer ![]() will remain the same for both problems. Consider minimizing
will remain the same for both problems. Consider minimizing ![]() subject to
subject to ![]() :
:
The true minimum value can be obtained by applying the function ![]() to the primal minimum value:
to the primal minimum value:
Since ![]() , solve the problem with
, solve the problem with ![]() and
and ![]() :
:
The optimal solution is the transformed minimum of the two solutions:
Transportation Problem (1)
Choose a number of units to transport for five goods by minimizing cost and maximizing profit. The cost and profit of transporting one unit of each good are:
The weight of each unit of goods and the maximum units available for transport are:
The minimum operating cost of running the truck is $2000 for the trip. The total transportation cost is:
The truck makes a minimum profit of $1000 if it rides empty. The total profit is:
The truck can carry a maximum of 8000 lbs. The constraints on the truck are:
The optimal mix of goods to transport if found by minimizing the ratio of cost to profit:
Production Planning (1)
Find the mix of four products to manufacture that minimize cost and maximize profit. The cost and profit of manufacturing one unit of each product are:
To manufacture each product, the company needs a combination of five resources, given by:
The maximum resources available are:
The constraints on the resources and products are:
The company has a minimum operating cost of $100. The total manufacturing cost is:
The total profit made by selling the products is:
To find out the maximum units to manufacture, minimize the ratio of cost to profit:
Resource Allocation (1)
Find the amount of electricity a company must send from its three power plants to four cities so as to maximize profit and minimize cost while meeting the cities' peak demands. The cost of transporting the 1 million kWh of electricity from each plant to the various cities is:
The profit that each power plant generates by selling 1 million kWh to each city is:
Let ![]() represent the amount of electricity sent by plant
represent the amount of electricity sent by plant ![]() to city
to city ![]() . The total cost of transporting electricity is
. The total cost of transporting electricity is ![]() and constructed using Inactive[Times]:
and constructed using Inactive[Times]:
The total profit made by the power company is ![]() and constructed using Inactive[Times]:
and constructed using Inactive[Times]:
The cities have a peak demand of 45, 20, 30, 30 million kWh, respectively:
The power plants can supply a minimum of 35, 50 and 40 million kWh of electricity, respectively:
The plants can only give and not receive power from the cities:
The optimal amount of electricity to send each city for each plant can be found by minimizing the ratio of cost to profit:
Blending Problems (1)
Find the mix of old alloys needed to make a new alloy containing at most 60% lead and at most 35% tin while minimizing cost and maximizing profit. The foundry has four existing old alloys containing tin and lead:
Let ![]() be the weight of the old alloy
be the weight of the old alloy ![]() . The new alloy is produced by a combination of the old alloys:
. The new alloy is produced by a combination of the old alloys:
The cost to acquire one pound of each of the four alloys is:
The cost to produce the new alloy is:
The foundry sells the new alloy for $200. The total profit that the foundry makes is:
The foundry must produce at least 15 lbs of the new alloy containing at most 60% lead and 35% tin:
The foundry has access to only 12, 15, 16 and 10 lbs of the four old alloys respectively:
The optimal mix of the old alloys to use can be found by minimizing the ratio of cost to profit:
Investment Problems (2)
Find the allocation of a maximum of $250,000 of capital to purchase two stocks and a bond such that the return on investment is maximized while reducing the cost of purchasing the stocks/bond. Let ![]() be the amount to invest in the two stocks and let
be the amount to invest in the two stocks and let ![]() be the amount to invest in the bond:
be the amount to invest in the bond:
The amount invested in the utilities stock cannot be more than $40,000 and pay a 9% dividend:
The amount invested in the bond must be at least $70,000 and pay 5% interest:
The total amount invested in the two stocks must be at least half the total amount invested:
The electronics stock pays a 4% dividend annually. The total return on investment is:
The cost associated with the investment is:
The optimal amount to be invested can be found by minimizing the ratio of cost to profit:
The total amount invested and the annual dividends received from the investments are:
Find the optimal combination of investments that yields maximum profit while minimizing cost. The net present value and the costs associated with each investment are:
Let ![]() be a decision variable such that
be a decision variable such that ![]() if investment
if investment ![]() is selected. The objective is to minimize costs while maximizing profits:
is selected. The objective is to minimize costs while maximizing profits:
There is a maximum $14,000 available for investing:
Solve the maximization problem to get the optimal combination of investments:
Set-Covering Problems (3)
Find the optimal combination of doctors a hospital ER must keep on call so that the ER can perform a list of procedures. Each doctor can only perform a certain number of procedures:
The cost (per hour) for keeping each doctor on call is:
Let ![]() be a decision vector such that
be a decision vector such that ![]() if doctor
if doctor ![]() is on call. The objective is to minimize cost while maximizing the total doctors present in the ER:
is on call. The objective is to minimize cost while maximizing the total doctors present in the ER:
At least one doctor must perform procedure ![]() :
:
Find the combination of doctors to keep on call:
Find the optimal number of fire stations that a city containing six districts must build such that there is at least one fire station within 15 minutes of each district. The time required to drive between districts is:
The cost (in millions of dollars) to build a fire station in each city is:
Let ![]() be a decision vector such that
be a decision vector such that ![]() if a fire station is built in district
if a fire station is built in district ![]() . The objective is to minimize the cost for the largest number of fire stations:
. The objective is to minimize the cost for the largest number of fire stations:
At least one fire station must be within 15 minutes of each district:
Find the districts in which a fire station will be built:
Find the optimal number of storage depots a company needs to build to distribute to six of its retail stores. The company has selected five possible sites. The cost to supply each store from each depot is:
The construction cost (in millions) for each depot is:
Let ![]() be a decision variable such that
be a decision variable such that ![]() if depot
if depot ![]() is built. Let
is built. Let ![]() represent the fraction of goods that depot
represent the fraction of goods that depot ![]() supplies to store
supplies to store ![]() . The total cost is:
. The total cost is:
The company expects to make a profit of $1 million from each depot by renting out unused space:
Each store must receive all the goods:
Only the depots that are built can supply the goods to the store:
Find which of the five depots should be constructed:
Traveling Salesman Problem (1)
Find the path that a salesman should take through ![]() cities such that each city is only visited once and that minimizes the distance and maximizes travel cost savings. Generate the locations:
cities such that each city is only visited once and that minimizes the distance and maximizes travel cost savings. Generate the locations:
Let ![]() be the distance between city
be the distance between city ![]() and city
and city ![]() . Let
. Let ![]() be a decision variable such that if
be a decision variable such that if ![]() , the path goes from city
, the path goes from city ![]() to city
to city ![]() :
:
The travel budget to go from one city to another is $15. If two cities are are within 50 miles, the salesman pays $5, else pays $10 flat rate. The total savings are:
The objective is to minimize distance while maximizing the savings:
The salesman can arrive from exactly one city and can depart to exactly one other city:
The salesman cannot arrive to one city and depart to the same city:
The salesman must travel to all the locations in a single tour:
The decision variable is a binary variable and the dummy variable is ![]() :
:
Properties & Relations (5)
LinearFractionalOptimization gives the global minimum of the objective function:
Minimize also gives global exact results for linear fractional optimization problems:
NMinimize can be used to obtain inexact results using global methods:
FindMinimum can be used to obtain inexact results using local methods:
LinearOptimization is a special case of LinearFractionalOptimization:
Possible Issues (6)
Constraints specified using strict inequalities may not be satisfied:
The minimum value of an empty set or infeasible problem is defined to be ![]() :
:
The minimizer is Indeterminate:
The minimum value for an unbounded set or unbounded problem is ![]() :
:
The minimizer is Indeterminate:
Dual related solution properties for mixed-integer problems may not be available:
Mixed-integer problems can only be solved in machine precision:
Constraints with complex values need to be specified using vector inequalities:
Just using GreaterEqual or LessEqual will not work:
Tech Notes
Related Guides
Text
Wolfram Research (2019), LinearFractionalOptimization, Wolfram Language function, https://reference.wolfram.com/language/ref/LinearFractionalOptimization.html (updated 2020).
CMS
Wolfram Language. 2019. "LinearFractionalOptimization." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/LinearFractionalOptimization.html.
APA
Wolfram Language. (2019). LinearFractionalOptimization. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LinearFractionalOptimization.html
BibTeX
@misc{reference.wolfram_2025_linearfractionaloptimization, author="Wolfram Research", title="{LinearFractionalOptimization}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/LinearFractionalOptimization.html}", note=[Accessed: 12-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_linearfractionaloptimization, organization={Wolfram Research}, title={LinearFractionalOptimization}, year={2020}, url={https://reference.wolfram.com/language/ref/LinearFractionalOptimization.html}, note=[Accessed: 12-March-2026]}