GeometricOptimization
GeometricOptimization[f,cons,vars]
求可最小化受正多项式约束条件 cons 限制的正多项式目标函数的变量 vars 的正值.
GeometricOptimization[{a0,b0},{{a1,b1},…},{aeq,beq}]
求可最小化受不等式约束条件 ![]() 和线性等式约束条件
和线性等式约束条件 ![]() 限制的
限制的 ![]() 的正向量 x=y.
的正向量 x=y.
GeometricOptimization[…,"prop"]
指定应返回解的属性 "prop".
更多信息和选项




- 几何优化亦称为几何规划 (GP) 或混合整数几何规划 (MIGP).
- 几何优化经常被用于最小化面积、体积或功率等量.
- 几何优化求的是能解原问题的
 :
: -
最小化 
受限于约束条件 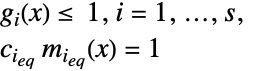
其中 
- 单项式是幂的积
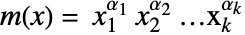 ,其中
,其中 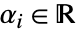 . 正多项式是单项式
. 正多项式是单项式 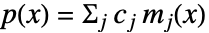 的正和,其中
的正和,其中 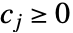 .
. - 广义正多项式
 是一个正多项式或广义多项式的组合:
是一个正多项式或广义多项式的组合: -
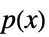
正多项式 
广义正多项式的和 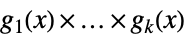
广义正多项式的积 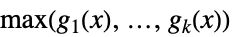
广义正多项式的最大值 
广义正多项式的正实数次幂 - 通过变换
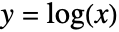 ,正多项式
,正多项式 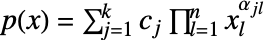 对应于一个
对应于一个 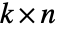 的矩阵
的矩阵 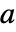 (其中
(其中 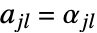 )和
)和  -向量
-向量 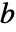 (其中
(其中 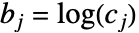 ),如下所示:
),如下所示: -
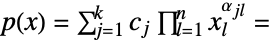
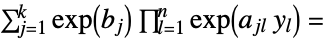
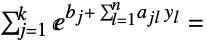
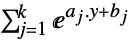
- 问题的等效表达形式是求
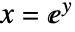 ,其中
,其中 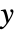 为问题的解:
为问题的解: -
最小化 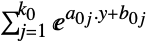
受限于约束条件 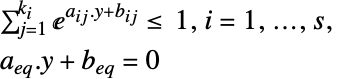
其中 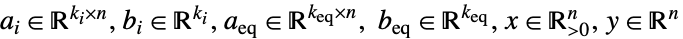
- 在 GeometricOptimization[{a0,b0},{{a1,b1},…},{aeq,beq}] 中,ai 应为
 的矩阵,bi 应为
的矩阵,bi 应为 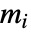 向量,aeq 应为一个
向量,aeq 应为一个 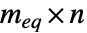 的矩阵,
的矩阵,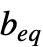 应为一个
应为一个 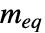 向量. 如果没有等式约束条件,可用 {} 给定{aeq,beq} 或省略.
向量. 如果没有等式约束条件,可用 {} 给定{aeq,beq} 或省略. - 原始最小化问题有相关的最大化问题,即拉格朗日对偶问题. 对偶最大值始终小于或等于原始最小值,因此它给出了下限. 对偶最大值点提供了有关原问题的信息,包括最小值对约束条件变化的敏感性.
- 几何优化有以下对偶问题:
-
最大化 
受限于约束条件 
其中 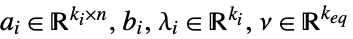
- 对于锥优化,强对偶性始终成立,这意味着如果原始最小化问题的解存在,那么对偶最大化问题的解也存在,并且对偶最大值等于原始最小值.
- 可能的解的属性 "prop" 包括:
-
"PrimalMinimizer" 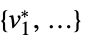
最小化 f 的变量值列表 vars={v1,…} "PrimalMinimizerRules" 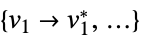
最小化 vars={v1,…} 的值的规则 "PrimalMinimizerVector" 
最小化 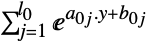 的向量
的向量"PrimalMinimumValue" 
最小值 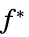
"DualMaximizer" 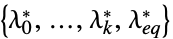
最大化 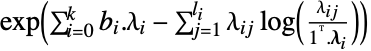 的向量
的向量 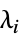 的列表
的列表"DualMaximumValue" 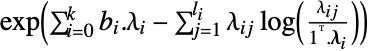
对偶最大值 "DualityGap" 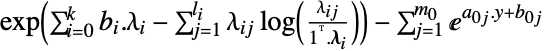
对偶值和原始最优值之间的差 "Slack" 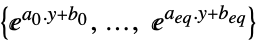
给出正多项式的每个单项式的值的向量 "ConstraintSensitivity" 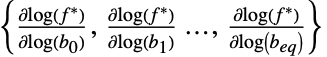
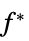 对约束条件扰动的敏感性
对约束条件扰动的敏感性"ConstraintMatrices" 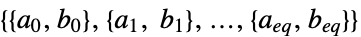
项 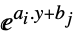 的矩阵
的矩阵"ObjectiveFunction" 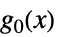
目标函数 "GeometricConstraints" 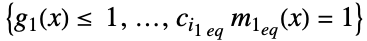
几何约束条件列表 {"prop1","prop2",…} 几个解的属性 - 可给出以下选项:
-
MaxIterations Automatic 使用的最大迭代次数 Method Automatic 使用的方法 PerformanceGoal $PerformanceGoal 优化的目标 Tolerance Automatic 内部比较采用的容差 - 计算受限于 MachinePrecision.
范例
打开所有单元关闭所有单元范围 (12)
基本用法 (4)
原始模型属性 (3)
对偶模型属性 (2)
用 ConicOptimization 形成的式子用中间变量 ![]() 替换了凸项
替换了凸项 ![]() ,添加了约束条件
,添加了约束条件 ![]() ,等价于先前使用的对偶指数锥约束条件;
,等价于先前使用的对偶指数锥约束条件;![]() 要求
要求 ![]() .
.
可以通过 "DualMaximizer" 属性更容易地获得 ![]() 和
和 ![]() :
:
原始最小值和对偶最大值相同,因为 GeometricOptimization 具有强对偶性. 它们的差被称为对偶间隙:
因为所有项都是单项式,所以所有矩阵 ![]() 只有一个行,对偶向量
只有一个行,对偶向量 ![]() 只有一个元素,所以
只有一个元素,所以 ![]() . 最大化
. 最大化 ![]() 相当于最小化
相当于最小化 ![]() ,由于指数是单调递增函数,因此相当于最小化
,由于指数是单调递增函数,因此相当于最小化 ![]() ,所以可用以下方式求解对偶问题:
,所以可用以下方式求解对偶问题:
敏感性属性 (3)
最大化一个开口盒子的体积,盒子的高度 ![]() 、宽度
、宽度 ![]() 和深度
和深度 ![]() 的约束条件为要使得盒子的成本小于 $100. 底部的成本为每单位面积 $10,侧面的成本为每单位面积 $1:
的约束条件为要使得盒子的成本小于 $100. 底部的成本为每单位面积 $10,侧面的成本为每单位面积 $1:
底部的成本是第二个元素的第一部分(第一个元素对应于目标). 敏感性为负的,因为 ![]() :
:
一个盒子,高度为 ![]() ,宽度为
,宽度为 ![]() ,深度为
,深度为 ![]() ,如果顶部和底部的面积和侧面的面积受约束条件而发生变化,求盒子的最大体积的相对变化. 最大化体积等同于最小化体积的倒数:
,如果顶部和底部的面积和侧面的面积受约束条件而发生变化,求盒子的最大体积的相对变化. 最大化体积等同于最小化体积的倒数:
将侧面的总面积限制为小于或等于 ![]() ,并将顶部和底部的面积限制为小于或等于
,并将顶部和底部的面积限制为小于或等于 ![]() :
:
与面积约束条件相关的是第二个和第三个(第一个与目标相关)元素:
应用 (16)
几何问题 (4)
矩阵问题 (2)
设计储存罐 (1)
平面规划 (1)
规划具有最小总面积的矩形平面,该矩形平面将 ![]() 个指定面积的矩形围在一起,限制这些矩形的长宽比、矩形之间的距离和相对位置.
个指定面积的矩形围在一起,限制这些矩形的长宽比、矩形之间的距离和相对位置.
用 Rectangle[{0,0},{H,W}] 描述大矩形,用 ri=Rectangle[{xi,yi},{xi+wi,yi+hi}], i=1,…,n 描述被围的小矩形.
可以用两个有向图来描述相对位置,用 ![]() 描述水平方向上的放置,用
描述水平方向上的放置,用 ![]() 描述垂直方向上的放置. 如果存在边 ij,则 ri 应在 rj 的左侧(或下方):
描述垂直方向上的放置. 如果存在边 ij,则 ri 应在 rj 的左侧(或下方):
令 ![]() 为矩形之间的最小间距. 当
为矩形之间的最小间距. 当 ![]() 有边 ij 时,矩形
有边 ij 时,矩形 ![]() 被限制为位于矩形
被限制为位于矩形 ![]() 的左侧,因而
的左侧,因而 ![]() . 当
. 当 ![]() 有边 ij 时,矩形
有边 ij 时,矩形 ![]() 被限制为位于矩形
被限制为位于矩形 ![]() 的下边,因而
的下边,因而 ![]() . 可用以下函数对图进行遍历并考虑可能位于平面边缘的矩形:
. 可用以下函数对图进行遍历并考虑可能位于平面边缘的矩形:
给定布局图、面积 ![]() 和
和 ![]() ,可通过使用 GeometricOptimization 的函数将规则合并起来:
,可通过使用 GeometricOptimization 的函数将规则合并起来:
结构型优化问题 (3)
设计能承受垂直载荷 ![]() 或水平载荷
或水平载荷 ![]() 的重量最小的桁架. 桁架的杆是空心管,内径为
的重量最小的桁架. 桁架的杆是空心管,内径为 ![]() ,外径为
,外径为 ![]() ,密度为
,密度为 ![]() :
:

用桁架的高度 ![]() 和宽度
和宽度 ![]() 定义杆的长度. 截面积为
定义杆的长度. 截面积为 ![]() . 目标是最小化重量:
. 目标是最小化重量:
杆上承受的总力不得超过允许的最大受力 ![]() ,其中
,其中 ![]() 为允许的最大应力:
为允许的最大应力:
要求空心管的壁厚最小. 可要求 ![]() (
(![]() ) 来实现. 杆的面积与半径之间的关系为
) 来实现. 杆的面积与半径之间的关系为 ![]() ,不是单项函数. 通过使用
,不是单项函数. 通过使用 ![]() 和约束条件
和约束条件 ![]() ,所得约束条件为单项式:
,所得约束条件为单项式:
设计能承受垂直载荷 ![]() 的重量最小的桁架. 已知桁架的高度
的重量最小的桁架. 已知桁架的高度 ![]() 和宽度
和宽度 ![]() . 节点
. 节点 ![]() 的垂直位置未知:
的垂直位置未知:
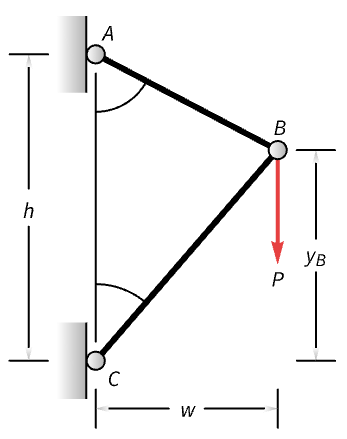
令 ![]() 分别为杆
分别为杆 ![]() 和
和 ![]() 的截面积,
的截面积,![]() 为杆的密度. 桁架的重量由下式给出:
为杆的密度. 桁架的重量由下式给出:
杆 ![]() 承受的是张力. 令
承受的是张力. 令 ![]() 为材料的拉伸应力. 杆
为材料的拉伸应力. 杆 ![]() 上承受的力不得超过允许的最大受力:
上承受的力不得超过允许的最大受力:
杆 ![]() 承受的是压力. 令
承受的是压力. 令 ![]() 为材料的抗压应力. 杆
为材料的抗压应力. 杆 ![]() 上承受的力不得超过允许的最大受力:
上承受的力不得超过允许的最大受力:
给定 ![]() 的值,可求解几何优化问题的的特定实例. 假设节点
的值,可求解几何优化问题的的特定实例. 假设节点 ![]() 的垂直位置必须在一定范围内,在该范围内求解:
的垂直位置必须在一定范围内,在该范围内求解:
设计一个自由端能承受垂直载荷 ![]() 的重量最小的悬臂. 悬臂由
的重量最小的悬臂. 悬臂由 ![]() 个单位长度的节段组成. 每个节段的宽度为
个单位长度的节段组成. 每个节段的宽度为 ![]() ,高度为
,高度为 ![]() :
:
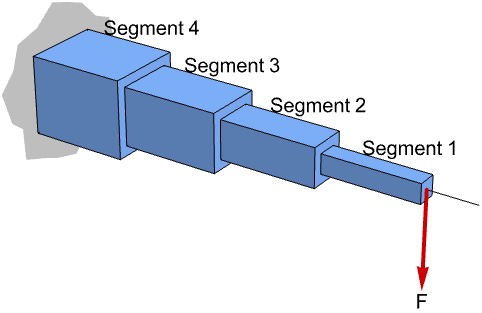
载荷使梁偏斜,在梁的每个节段上产生应力 ![]() . 应力必须小于允许的最大应力
. 应力必须小于允许的最大应力 ![]() :
:
电路问题 (3)
设计数字电路门的大小:求给定电路中受功率和面积限制的门的最佳尺寸,以最小化电路中的延迟. 考虑由七个门组成的电路:
门 ![]() 转换时损失的能量与比例因子
转换时损失的能量与比例因子 ![]() 成正比,门转换时的转换频率
成正比,门转换时的转换频率 ![]() 和能量损失
和能量损失 ![]() 为:
为:
门 ![]() 的输入电容
的输入电容 ![]() ,门 6 和 7 除外,它们的输入电容为 10:
,门 6 和 7 除外,它们的输入电容为 10:
门 ![]() 的电容是与其输出相连的门的输入电容之和,输出门 6 和 7 除外,它们的电容与其输入电容相同:
的电容是与其输出相连的门的输入电容之和,输出门 6 和 7 除外,它们的电容与其输入电容相同:
目标是使电路中可遍历的所有路径组合的最坏情况下的延迟最小化:
在已知电容的电路中,求 ![]() 段电线的宽度. 下面的网络中有五段电线:
段电线的宽度. 下面的网络中有五段电线:
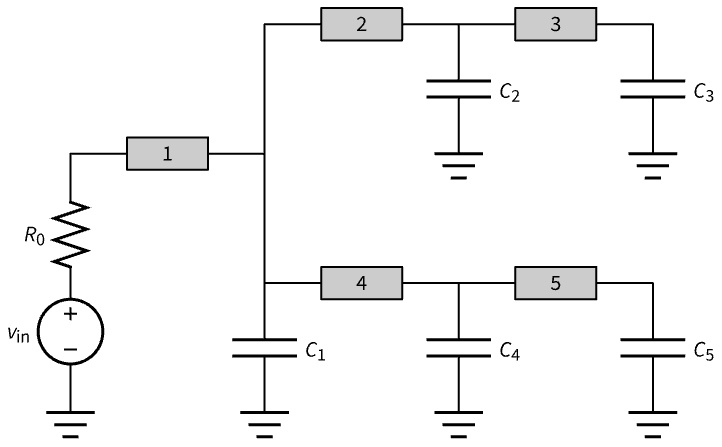
每段电线的电阻为 ![]() ,电容为
,电容为 ![]() ,其中
,其中 ![]() 为正常数,具体取决于电线的特性,
为正常数,具体取决于电线的特性,![]() 是电线的长度,宽度为
是电线的长度,宽度为 ![]() :
:
使用 ![]() 模型,用一个电阻和电容来模拟电线. 所得网络为电阻器-电容器网络:
模型,用一个电阻和电容来模拟电线. 所得网络为电阻器-电容器网络:
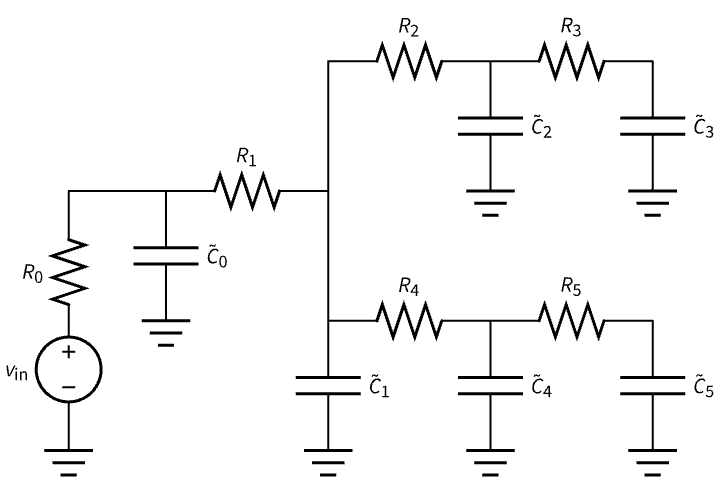
通过将各个网络电容与电线的电容 ![]() 相加,可以得到模型的新电容:
相加,可以得到模型的新电容:
Elmore 延迟测量的是电压变化并收敛到新值所造成的延迟. 每个电容 ![]() 的 Elmore 延迟为
的 Elmore 延迟为 ![]() ,其中
,其中 ![]() 是电容
是电容 ![]() 和
和 ![]() 之间的一组电阻:
之间的一组电阻:
求晶体管的最佳掺杂分布,以最小化基区渡越时间. 令 ![]() 为掺杂分布,其中
为掺杂分布,其中 ![]() 为基区宽度. 令
为基区宽度. 令 ![]() 为基区渡越时间.
为基区渡越时间. ![]() 给出了作为
给出了作为 ![]() 的函数的简化模型,其中
的函数的简化模型,其中 ![]() 是一个常数. 令
是一个常数. 令 ![]() ;可用
;可用 ![]() 个等距点将积分离散化:
个等距点将积分离散化:
文本
Wolfram Research (2020),GeometricOptimization,Wolfram 语言函数,https://reference.wolfram.com/language/ref/GeometricOptimization.html.
CMS
Wolfram 语言. 2020. "GeometricOptimization." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/GeometricOptimization.html.
APA
Wolfram 语言. (2020). GeometricOptimization. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/GeometricOptimization.html 年