Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

GraphDiameter

GraphDiameter[g]

给出图 g 中任意一对顶点之间的最大距离.

GraphDiameter[{vw,…}]

使用规则 vw 指定图 g.

更多信息和选项

可以给出下列选项：
EdgeWeight Automatic 各边权值

Method Automatic 使用的方法
在缺省设置 EdgeWeight->Automatic 下，如果可用，边的权值取图 g 的 EdgeWeight；否则值为 1.
可能的 Method 设置包括 "Dijkstra"、"FloydWarshall"、"Johnson" 和 "PseudoDiameter".
GraphDiameter 可处理无向图、有向图、加权图、多图和混合图.

范例

打开所有单元关闭所有单元

基本范例 (1)

给出一个完全图的直径：

范围 (7)

GraphDiameter 适用于无向图：

有向图：

加权图：

多图：

混合图：

使用规则指定图：

GraphDiameter 适用于大规模图：

应用 (2)

显示两个 Petersen 图中的直径：

对于一个 CompleteGraph，直径为1：

对于一个大小为的 PathGraph，直径是：

对于一个大小为的 CycleGraph，直径是：

对于一个大小为5或者更大的 WheelGraph，直径是 2：

一个大小为4的 WheelGraph 是一个完全图，所以直径为1：

对于一个大小为 {m,n} 的 GridGraph，直径是：

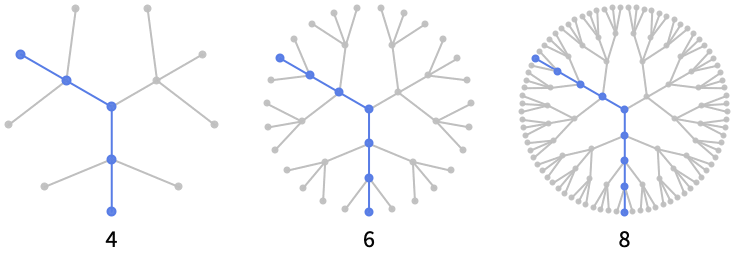
对于一棵深度为的 CompleteKaryTree 树，直径是：

求在一个家庭聚会网络中分离开两个人的最大步骤数：

属性和关系 (3)

对于一个连通图，直径可以通过 VertexEccentricity 计算：

如果一个简单图的直径大于3，那么它的补图具有小于3的直径：

当把每条边的方向取反，图的直径不会发生改变：

顶部