WOLFRAM

Wolfram Language & System Documentation Center

GroupElementFromWord[group,w]

returns the element of group determined by the word w in the generators of group.

Details
Details and Options Details and Options
Examples  
Basic Examples  
Scope  
Properties & Relations  
See Also
Tech Notes
Related Guides
History
Cite this Page

GroupElementFromWord

GroupElementFromWord[group,w]

returns the element of group determined by the word w in the generators of group.

Details

  • In GroupElementFromWord[group,w], the word w must be a list of nonzero integers {m1,…,mk} representing generators in the list returned by GroupGenerators[group]. A positive integer 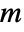in the word represents the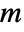 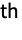^(th) generator, and a negative integer 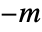represents the inverse of the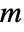 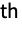^(th) generator.

Examples

open all close all

Basic Examples  (1)

For a given list of group generators, this word represents the product of the first generator with itself and then with inverse of the second generator:

For the dihedral group of order 16, the word corresponds to the element:

The same result can be obtained by multiplying the generators explicitly:

Scope  (1)

Reconstruct a permutation from its word in a list of generators:

If the generators are given in permutation list form, then the result is also in the same form:

Properties & Relations  (3)

GroupElementToWord constructs the word for a given group element:

The group element can then be reconstructed with GroupElementFromWord:

The empty word always corresponds to the identity element for any group:

GroupElementFromWord is equivalent to the following function:

Wolfram Research (2012), GroupElementFromWord, Wolfram Language function, https://reference.wolfram.com/language/ref/GroupElementFromWord.html.

Text

Wolfram Research (2012), GroupElementFromWord, Wolfram Language function, https://reference.wolfram.com/language/ref/GroupElementFromWord.html.

CMS

Wolfram Language. 2012. "GroupElementFromWord." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GroupElementFromWord.html.

APA

Wolfram Language. (2012). GroupElementFromWord. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GroupElementFromWord.html

BibTeX

@misc{reference.wolfram_2025_groupelementfromword, author="Wolfram Research", title="{GroupElementFromWord}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/GroupElementFromWord.html}", note=[Accessed: 16-August-2025]}

BibLaTeX

@online{reference.wolfram_2025_groupelementfromword, organization={Wolfram Research}, title={GroupElementFromWord}, year={2012}, url={https://reference.wolfram.com/language/ref/GroupElementFromWord.html}, note=[Accessed: 16-August-2025]}