GroupElementToWord[group,g]
decomposes the group element g as a product of generators of group.


GroupElementToWord
GroupElementToWord[group,g]
decomposes the group element g as a product of generators of group.
Details and Options
- The group element g must belong to the given group.
- GroupElementToWord[group,g] gives the word of g in the form of a list of nonzero integers {m1,…,mk} representing generators in the list returned by GroupGenerators[group]. A positive integer
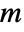 in the word represents the
in the word represents the 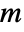
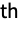 generator, and a negative integer
generator, and a negative integer 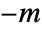 represents the inverse of the
represents the inverse of the 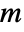
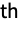 generator.
generator. - GroupElementToWord takes the following options:
-
GroupActionBase Automatic group action base MaxIterations Automatic maximum number of iterations Method Automatic method to use
Examples
open all close allBasic Examples (1)
Scope (2)
Options (3)
GroupBaseAction (1)
MaxIterations (1)
Method (1)
GroupElementToWord uses the Minkwitz algorithm, with a number of parameters:
Applications (1)
Properties & Relations (4)
GroupElementFromWord reconstructs the original group element from the word:
Identity generators are not used, but affect the indexing of the other generators:
The identity permutation always corresponds to the empty word:
The element must belong to the group:
Neat Examples (1)
The group of a 3×3×3 Rubik's cube is usually given in terms of six generators:
However, one of them is redundant, and the group can actually be constructed with only five face rotations:
This is a possible word expressing the sixth rotation in terms of the first five and their inverses:
After removing the generators corresponding to opposite faces, the remaining four still move all facelets, but now they only generate a subgroup of index 2048:
This is because there are two disconnected sets of edge facelets:
Tech Notes
Related Guides
History
Text
Wolfram Research (2012), GroupElementToWord, Wolfram Language function, https://reference.wolfram.com/language/ref/GroupElementToWord.html.
CMS
Wolfram Language. 2012. "GroupElementToWord." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GroupElementToWord.html.
APA
Wolfram Language. (2012). GroupElementToWord. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GroupElementToWord.html
BibTeX
@misc{reference.wolfram_2025_groupelementtoword, author="Wolfram Research", title="{GroupElementToWord}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/GroupElementToWord.html}", note=[Accessed: 25-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_groupelementtoword, organization={Wolfram Research}, title={GroupElementToWord}, year={2012}, url={https://reference.wolfram.com/language/ref/GroupElementToWord.html}, note=[Accessed: 25-January-2026]}