HeunC[q,α,γ,δ,ϵ,z]
gives the confluent Heun function.




HeunC
HeunC[q,α,γ,δ,ϵ,z]
gives the confluent Heun function.
Details

- HeunC belongs to the Heun class of functions and occurs in quantum mechanics, mathematical physics and applications.
- Mathematical function, suitable for both symbolic and numerical manipulation.
- HeunC[q,α,γ,δ,ϵ,z] satisfies the confluent Heun differential equation
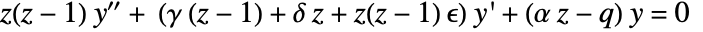 .
. - The HeunC function is the regular solution of the confluent Heun equation that satisfies the condition HeunC[q,α,γ,δ,ϵ,0]1.
- HeunC has a branch cut discontinuity in the complex
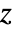 plane running from
plane running from 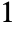 to
to 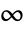 .
. - For certain special arguments, HeunC automatically evaluates to exact values.
- HeunC can be evaluated for arbitrary complex parameters.
- HeunC can be evaluated to arbitrary numerical precision.
- HeunC automatically threads over lists.
Examples
open all close allScope (26)
Numerical Evaluation (8)
Specific Values (3)
Visualization (5)
Function Properties (1)
HeunC can be simplified to Hypergeometric1F1 function in the following case:
Differentiation (2)
The ![]() -derivative of HeunC is HeunCPrime:
-derivative of HeunC is HeunCPrime:
Higher derivatives of HeunC are calculated using HeunCPrime:
Integration (3)
Applications (4)
Solve the confluent Heun differential equation using DSolve:
Solve the initial value problem for the confluent Heun differential equation:
Plot the solution for different values of the accessory parameter q:
Directly solve the confluent Heun differential equation:
HeunC with specific parameters solves the Mathieu equation:
Construct the general solution of the Mathieu equation in terms of HeunC functions:
Properties & Relations (3)
HeunC is analytic at the origin:
![]() is a singular point of the HeunC function:
is a singular point of the HeunC function:
Except for this singular point, HeunC can be calculated at any finite complex ![]() :
:
The derivative of HeunC is HeunCPrime:
Possible Issues (1)
HeunC cannot be evaluated if ![]() is a nonpositive integer (so-called logarithmic cases):
is a nonpositive integer (so-called logarithmic cases):
Related Guides
History
Text
Wolfram Research (2020), HeunC, Wolfram Language function, https://reference.wolfram.com/language/ref/HeunC.html.
CMS
Wolfram Language. 2020. "HeunC." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/HeunC.html.
APA
Wolfram Language. (2020). HeunC. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HeunC.html
BibTeX
@misc{reference.wolfram_2025_heunc, author="Wolfram Research", title="{HeunC}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/HeunC.html}", note=[Accessed: 13-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_heunc, organization={Wolfram Research}, title={HeunC}, year={2020}, url={https://reference.wolfram.com/language/ref/HeunC.html}, note=[Accessed: 13-January-2026]}