HeunG[a,q,α,β,γ,δ,z]
gives the general Heun function.




HeunG
HeunG[a,q,α,β,γ,δ,z]
gives the general Heun function.
Details

- HeunG belongs to the Heun class of functions, directly generalizes the Hypergeometric2F1 function and occurs in quantum mechanics, mathematical physics and applications.
- Mathematical function, suitable for both symbolic and numerical manipulation.
- HeunG[a,q,α,β,γ,δ,z] satisfies the general Heun differential equation
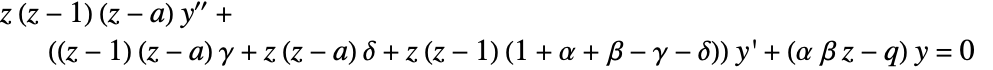 .
. - The HeunG function is the regular solution of the general Heun equation that satisfies the condition HeunG[a,q,α,β,γ,δ,0]1.
- HeunG has one branch cut discontinuity in the complex
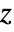 plane running from
plane running from 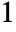 to
to 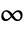 and one running from
and one running from 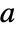 to DirectedInfinity[a].
to DirectedInfinity[a]. - For certain special arguments, HeunG automatically evaluates to exact values.
- HeunG can be evaluated for arbitrary complex parameters.
- HeunG can be evaluated to arbitrary numerical precision.
- HeunG automatically threads over lists.
- HeunG[a,q,α,β,γ,δ,z] specializes to Hypergeometric2F1[α,β,γ,z] if
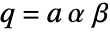 and
and 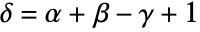 or
or 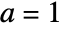 and
and 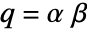 .
.
Examples
open all close allScope (37)
Numerical Evaluation (10)
The precision of the output tracks the precision of the input:
HeunG can take one or more complex number parameters:
HeunG can take complex number arguments:
Finally, HeunG can take all complex number input:
Evaluate HeunG efficiently at high precision:
Evaluate HeunG for points at branch cut ![]() to
to ![]() :
:
Evaluate HeunG for points on a branch cut from ![]() to DirectedInfinity[a]:
to DirectedInfinity[a]:
Compute the elementwise values of an array:
Or compute the matrix HeunG function using MatrixFunction:
Specific Values (8)
Value of HeunG at origin:
Value of HeunG at the regular singular point ![]() is indeterminate:
is indeterminate:
Value of HeunG at the regular singular point ![]() is indeterminate:
is indeterminate:
Values of HeunG in "logarithmic" cases, for nonpositive integer ![]() , are not determined:
, are not determined:
Value of HeunG is indeterminate if ![]() :
:
HeunG automatically evaluates to the Hypergeometric2F1 function if ![]() and
and ![]() :
:
HeunG automatically evaluates to the Hypergeometric2F1 function if ![]() and
and ![]() :
:
HeunG automatically evaluates to simpler functions for certain parameters:
Visualization (5)
Function Properties (3)
Hypergeometric2F1 is a special case of HeunG:
HeunG can be simplified to the Hypergeometric2F1 function with nonlinear argument:
HeunG can be simplified to rational functions in special cases:
Differentiation (4)
The ![]() -derivative of HeunG is HeunGPrime:
-derivative of HeunG is HeunGPrime:
Higher derivatives of HeunG are calculated using HeunGPrime:
Derivatives of HeunG for specific cases of parameters:
Higher derivatives of HeunG involving specific cases of parameters:
Integration (3)
Applications (5)
Solve the general Heun differential equation using DSolve:
Plot the solution for different initial conditions:
Solve the initial value problem:
Plot the solution for different values of the accessory parameter q:
Solve the Lamé differential equation in terms of HeunG:
Plot the absolute value of the solution for different h:
Stationary 1D Schrödinger equation for this infinite potential well is solved in terms of HeunG:
The fundamental solution of the Schrödinger equation in terms of HeunG:
Verify this solution by direct substitution:
The general form of a second-order Fuchsian equation with four regular singularities at ![]() and exponent parameters
and exponent parameters ![]() , subject to the constraint
, subject to the constraint ![]() :
:
Construct two linearly independent solutions in terms of HeunG:
Properties & Relations (6)
HeunG is analytic at the origin:
![]() and
and ![]() are singular points of the HeunG function:
are singular points of the HeunG function:
Except for these two singular points, HeunG can be calculated at any finite complex ![]() :
:
The derivative of HeunG is HeunGPrime:
HeunG is symmetric in the parameters ![]() and
and ![]() :
:
Four equivalent expressions for HeunG, corresponding to parameter transformations that leave the argument ![]() and singular point
and singular point ![]() invariant:
invariant:
Use Series to show that the series expansions of the last three expressions at ![]() agree with that of the first:
agree with that of the first:
Six equivalent expressions for HeunG, corresponding to argument transformations that leave the parameters ![]() and
and ![]() invariant:
invariant:
Use Series to show that the series expansions of the last five expressions at ![]() agree with that of the first:
agree with that of the first:
Possible Issues (2)
Neat Examples (1)
Create a table of some special cases for HeunG :
Related Guides
History
Text
Wolfram Research (2020), HeunG, Wolfram Language function, https://reference.wolfram.com/language/ref/HeunG.html.
CMS
Wolfram Language. 2020. "HeunG." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/HeunG.html.
APA
Wolfram Language. (2020). HeunG. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HeunG.html
BibTeX
@misc{reference.wolfram_2025_heung, author="Wolfram Research", title="{HeunG}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/HeunG.html}", note=[Accessed: 06-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_heung, organization={Wolfram Research}, title={HeunG}, year={2020}, url={https://reference.wolfram.com/language/ref/HeunG.html}, note=[Accessed: 06-March-2026]}