LameC[ν,j,z,m]
gives the ![]()
![]() Lamé function
Lamé function ![]() of order
of order ![]() with elliptic parameter
with elliptic parameter ![]() .
.




LameC
LameC[ν,j,z,m]
gives the ![]()
![]() Lamé function
Lamé function ![]() of order
of order ![]() with elliptic parameter
with elliptic parameter ![]() .
.
Details

- LameC belongs to the Lamé class of functions and solves boundary-value problems for Laplace's equation in ellipsoidal and spheroconal coordinates, as well as occurring in other problems of mathematical physics and quantum mechanics.
- Mathematical function, suitable for both symbolic and numerical manipulation.
- LameC[ν,j,z,m] satisfies the Lamé differential equation
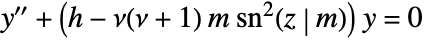 , with the Lamé eigenvalue
, with the Lamé eigenvalue 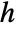 given by LameEigenvalueA[ν,j,m], and where
given by LameEigenvalueA[ν,j,m], and where ![TemplateBox[{z, m}, JacobiSN] TemplateBox[{z, m}, JacobiSN]](Files/LameC.en/8.png) is the Jacobi elliptic function JacobiSN[z,m].
is the Jacobi elliptic function JacobiSN[z,m]. - For certain special arguments, LameC automatically evaluates to exact values.
- LameC can be evaluated to arbitrary numerical precision for an arbitrary complex argument.
- LameC automatically threads over lists.
- LameC[ν,0,z,0]=
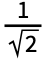 and LameC[ν,j,z,0]=Cos[j(
and LameC[ν,j,z,0]=Cos[j(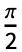 -z)].
-z)]. - LameC[ν,j,z,m] is proportional to HeunG[a,q,α,β,γ,δ,ξ], where
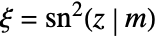 , if the parameters of HeunG are specialized as follows:
, if the parameters of HeunG are specialized as follows: 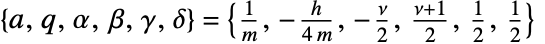 .
.
Examples
open all close allBasic Examples (3)
Scope (27)
Numerical Evaluation (5)
Specific Values (3)
Visualization (6)
Plot the first three even LameC functions:
Plot the first three odd LameC functions:
Plot the absolute value of the LameC function for complex parameters:
Plot LameC as a function of its first parameter ![]() :
:
Plot LameC as a function of ![]() and elliptic parameter
and elliptic parameter ![]() :
:
Plot the family of LameC functions for different values of the elliptic parameter ![]() :
:
Function Properties (2)
Differentiation (3)
The ![]() -derivative of LameC is LameCPrime:
-derivative of LameC is LameCPrime:
Higher derivatives of LameC are calculated using LameCPrime:
Derivatives of LameC for specific cases of parameters:
Integration (3)
Series Expansions (3)
Function Representations (2)
Applications (1)
LameC solves the Lamé differential equation when h=LameEigenvalueA[ν,j,m]:
Properties & Relations (2)
LameC is an even function when ![]() is a non-negative even integer:
is a non-negative even integer:
LameC is an odd function when ![]() is a positive odd integer:
is a positive odd integer:
Use FunctionExpand to expand LameC for integer values of ![]() and
and ![]() :
:
See Also
Related Guides
History
Text
Wolfram Research (2020), LameC, Wolfram Language function, https://reference.wolfram.com/language/ref/LameC.html.
CMS
Wolfram Language. 2020. "LameC." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LameC.html.
APA
Wolfram Language. (2020). LameC. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LameC.html
BibTeX
@misc{reference.wolfram_2025_lamec, author="Wolfram Research", title="{LameC}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/LameC.html}", note=[Accessed: 25-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_lamec, organization={Wolfram Research}, title={LameC}, year={2020}, url={https://reference.wolfram.com/language/ref/LameC.html}, note=[Accessed: 25-January-2026]}