その大きさが定まらない数値的な量を表すシンボルである.


Indeterminate
その大きさが定まらない数値的な量を表すシンボルである.
詳細
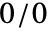 のような計算はIndeterminateを生成する.
のような計算はIndeterminateを生成する.- Indeterminateが属性NumericFunctionを持つ任意の関数の引数として用いられた場合,結果はIndeterminateとなる. »
- 演算がその結果として初めてIndeterminateを発生したとき,メッセージが作成される.
例題
すべて開く すべて閉じる例 (2)
スコープ (3)
一般化と拡張 (1)
Indeterminateを含む数学操作はIndeterminateを生む:
Indeterminateはリストに対して縫い込まれる:
アプリケーション (1)
精度の限界を超える桁はIndeterminateとみなされる:
特性と関係 (1)
Indeterminateは数ではない:
考えられる問題 (5)
Limitを使って値を解く:
この特定のパラメータ値はIndeterminateの結果を返す:
Limitを使って値を解く:
Indeterminateはそれ自身と等しくならない:
SameQをIndeterminateの検証に使う:
特別な評価動作を持つ関数のIndeterminateは,気付かれないことがある:
テクニカルノート
-
▪
- 不定形・無限大
関連するガイド
-
▪
- 数学定数
履歴
1988 で導入 (1.0)
テキスト
Wolfram Research (1988), Indeterminate, Wolfram言語関数, https://reference.wolfram.com/language/ref/Indeterminate.html.
CMS
Wolfram Language. 1988. "Indeterminate." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Indeterminate.html.
APA
Wolfram Language. (1988). Indeterminate. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Indeterminate.html
BibTeX
@misc{reference.wolfram_2025_indeterminate, author="Wolfram Research", title="{Indeterminate}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/Indeterminate.html}", note=[Accessed: 11-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_indeterminate, organization={Wolfram Research}, title={Indeterminate}, year={1988}, url={https://reference.wolfram.com/language/ref/Indeterminate.html}, note=[Accessed: 11-February-2026]}