InverseEllipticNomeQ

InverseEllipticNomeQ[q]

楕円関数のノーム q に対応したパラメータ m を与える．

詳細

  • 記号操作・数値操作の両方に適した数学関数である．
  • InverseEllipticNomeQ[q]は，EllipticNomeQ[m]を q に等しいものとするパラメータ m の固有な値を与える．
  • ノーム q は常に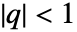を満たさなければならない．
  • InverseEllipticNomeQは任意の数値精度で評価できる．
  • InverseEllipticNomeQは自動的にリストに縫い込まれる．

例題

すべて開くすべて閉じる

例  (4)

数値的に評価する：

実数の部分集合上でプロットする：

原点における級数展開：

特異点における漸近展開：

スコープ  (26)

数値評価  (6)

数値的に評価する：

高精度で評価する：

出力精度は入力精度に従う：

複素数入力：

高精度で効率的に評価する：

Aroundを使って平均的な場合の統計区間を計算する：

配列の要素ごとの値を計算する：

MatrixFunctionを使って行列のInverseEllipticNomeQ関数を計算することもできる：

特定の値  (4)

固定点における値：

記号的に評価する：

ゼロにおける値：

InverseEllipticNomeQ[x]=0.9となるような の値を求める：

可視化  (2)

InverseEllipticNomeQ関数をさまざまなパラメータについてプロットする：

TemplateBox[{z}, InverseEllipticNomeQ]の実部をプロットする：

TemplateBox[{z}, InverseEllipticNomeQ]の虚部をプロットする：

関数の特性  (10)

InverseEllipticNomeQの実領域：

InverseEllipticNomeQの複素領域：

InverseEllipticNomeQは要素単位でリストに縫い込まれる：

InverseEllipticNomeQはその実領域上で解析関数である：

一般に，特異点と不連続点の両方を持つ：

InverseEllipticNomeQはその実領域上で非減少である：

InverseEllipticNomeQは単射である：

InverseEllipticNomeQは全射ではない：

InverseEllipticNomeQは非負でも非正でもない：

InverseEllipticNomeQはその実領域上で凹である：

TraditionalFormによる表示：

微分  (2)

についての一次導関数：

についての高次導関数：

についての高次微分をプロットする：

級数展開  (2)

Seriesを使ってテイラー(Taylor)展開を求める：

の周りの最初の3つの近似をプロットする：

生成点におけるテイラー展開：

一般化と拡張  (1)

InverseEllipticNomeQはベキ級数に適用することができる：

アプリケーション  (4)

楕円関数の恒等式中で，楕円モジュールとノルム間で変換する：

単位長の有限の容器中における原子1つの単原子気体についての分配関数：

n 個のボーズ粒子の分配関数を作る：

平均エネルギーを計算しプロットする：

InverseEllipticNomeQはモジュール関数である．モジュール方程式のアプローチを作る：

方程式の過剰決定系を構成し，解く：

これは二階モジュール方程式である：

Seriesを使って確かめる：

ワイエルシュトラス不変量で指定された楕円曲線に対応する係数を求める：

InverseEllipticNomeQを使って係数を計算する：

特性と関係  (5)

逆関数で構成する：

導関数を求める：

超越関数を記号的に解く：

超越方程式の根を数値的に求める：

q 級数との関係：

考えられる問題  (2)

分析性の領域外では，InverseEllipticNomeQは評価されずに残る：

InverseEllipticNomeQは一価でEllipticNomeQは多価である：

Wolfram Research (1996), InverseEllipticNomeQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/InverseEllipticNomeQ.html.

テキスト

Wolfram Research (1996), InverseEllipticNomeQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/InverseEllipticNomeQ.html.

CMS

Wolfram Language. 1996. "InverseEllipticNomeQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InverseEllipticNomeQ.html.

APA

Wolfram Language. (1996). InverseEllipticNomeQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseEllipticNomeQ.html

BibTeX

@misc{reference.wolfram_2024_inverseellipticnomeq, author="Wolfram Research", title="{InverseEllipticNomeQ}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/InverseEllipticNomeQ.html}", note=[Accessed: 04-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_inverseellipticnomeq, organization={Wolfram Research}, title={InverseEllipticNomeQ}, year={1996}, url={https://reference.wolfram.com/language/ref/InverseEllipticNomeQ.html}, note=[Accessed: 04-November-2024 ]}