JacobiSymbol

JacobiSymbol[n,m]

ヤコビの記号を与える．

詳細

  • 記号操作・数値操作の両方に適した数学的整数関数である．
  • 素である m について，ヤコビの記号はルジャンドル(Legendre)の記号に還元される．ルジャンドルの記号は，n が m の法の二次剰余であるかどうかに依存し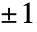，と等しい．
  • JacobiSymbolは，自動的にリストに縫い込まれる．

例題

すべて開くすべて閉じる

例  (2)

ヤコビの記号を計算する：

この数列を最後の引数についてプロットする：

スコープ  (3)

大きい引数について評価する：

第2引数は偶数でもよい：

TraditionalFormによる表示：

一般化と拡張  (2)

JacobiSymbolは，リストや配列に対して要素単位で適用される：

JacobiSymbolは，負の第1引数を取ることができる：

アプリケーション  (5)

オイラ–ヤコビの擬似素数を求める：

ガウスの相反則：

離散フーリエ変換の固有ベクトルを構築する：

ガウスの総和を閉じた形で評価する：

ヤコビの記号の自明ではない値をプロットする：

特性と関係  (1)

JacobiSymbolを含む方程式を簡約する：

おもしろい例題  (1)

2を法としたJacobiSymbolの連続する差分：

Wolfram Research (1988), JacobiSymbol, Wolfram言語関数， https://reference.wolfram.com/language/ref/JacobiSymbol.html.

テキスト

Wolfram Research (1988), JacobiSymbol, Wolfram言語関数， https://reference.wolfram.com/language/ref/JacobiSymbol.html.

CMS

Wolfram Language. 1988. "JacobiSymbol." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/JacobiSymbol.html.

APA

Wolfram Language. (1988). JacobiSymbol. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/JacobiSymbol.html

BibTeX

@misc{reference.wolfram_2024_jacobisymbol, author="Wolfram Research", title="{JacobiSymbol}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/JacobiSymbol.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_jacobisymbol, organization={Wolfram Research}, title={JacobiSymbol}, year={1988}, url={https://reference.wolfram.com/language/ref/JacobiSymbol.html}, note=[Accessed: 21-November-2024 ]}