JordanModelDecomposition

JordanModelDecomposition[ssm]

状態空間モデル ssm のジョルダン(Jordan)分解を与える．

詳細

  • 結果はリスト{p,jc}である．ただし，p は相似行列，jc は ssm のジョルダン正準形である．
  • 状態空間モデル ssm はStateSpaceModel[{a,b,c,d}]として与えられる．ただし，a，b，c，d は連続時間系あるいは離散時間系の状態，入力，出力，伝送行列を表す．
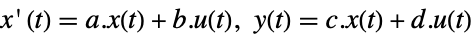
  • 連続時間系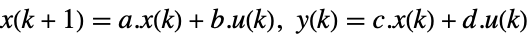
    離散時間系
  • 変換 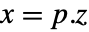( 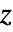は新たな状態ベクトル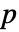， は 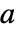の線形独立の固有ベクトルをスパンする相似行列）は，系をジョルダン正準形に変換する．
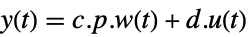
  • w'(t)=TemplateBox[{p}, Inverse].a.p.w(t)+TemplateBox[{p}, Inverse].b.u(t), 連続時間系
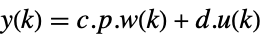
    w(k+1)=TemplateBox[{p}, Inverse].a.p.w(k)+TemplateBox[{p}, Inverse].b.u(k),離散時間系
  • 新たな状態行列 TemplateBox[{p}, Inverse].a.p はもとの状態行列 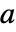のジョルダン正凖形である．

例題

すべて開くすべて閉じる

例  (1)

状態空間モデルのジョルダン分解を計算する：

スコープ  (4)

二次系のジョルダン分解：

離散時間系のジョルダン分解：

二次ブロックで複素数極を与える変換：

ジョルダンブロックには繰り返し極が現れる：

アプリケーション  (2)

のジョルダンブロックが明らかな固有値を持ち，各ジョルダンブロックの最終行に対応する の行が零ではないとき，かつそのときに限り，その系は可制御である：

のジョルダンブロックが明らかな固有値を持ち，各ジョルダンブロックの第1行に対応する の列が零ではないとき，かつそのときに限り，その系は可観測である：

特性と関係  (3)

ジョルダン正凖形では，固有値は状態行列の対角に沿っている：

ジョルダン正凖形は相似変換を介してもとの系に関連している：

状態空間モデルのジョルダン正凖形はその状態行列のジョルダン分解に関連した相似変換である：

考えられる問題  (1)

JordanModelDecompositionはディスクリプタ系をサポートしない：

KroneckerModelDecompositionを使って系のモードを分離する：

Wolfram Research (2010), JordanModelDecomposition, Wolfram言語関数， https://reference.wolfram.com/language/ref/JordanModelDecomposition.html.

テキスト

Wolfram Research (2010), JordanModelDecomposition, Wolfram言語関数， https://reference.wolfram.com/language/ref/JordanModelDecomposition.html.

CMS

Wolfram Language. 2010. "JordanModelDecomposition." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/JordanModelDecomposition.html.

APA

Wolfram Language. (2010). JordanModelDecomposition. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/JordanModelDecomposition.html

BibTeX

@misc{reference.wolfram_2024_jordanmodeldecomposition, author="Wolfram Research", title="{JordanModelDecomposition}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/JordanModelDecomposition.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_jordanmodeldecomposition, organization={Wolfram Research}, title={JordanModelDecomposition}, year={2010}, url={https://reference.wolfram.com/language/ref/JordanModelDecomposition.html}, note=[Accessed: 21-November-2024 ]}