KalmanEstimator

KalmanEstimator[ssm,{w,v}]

constructs the Kalman estimator for the StateSpaceModel ssm with process and measurement noise covariance matrices w and v.

KalmanEstimator[ssm,{w,v,h}]

includes the cross-covariance matrix h.

KalmanEstimator[{ssm,sensors},{…}]

specifies sensors as the noisy measurements of ssm.

KalmanEstimator[{ssm,sensors,dinputs},{…}]

specifies dinputs as the deterministic inputs of ssm.

Details and Options

  • The standard state-space model ssm can be given as StateSpaceModel[{a,b,c,d}], where a, b, c, and d represent the state, input, output, and transmission matrices in either a continuous-time or a discrete-time system:
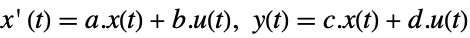
  • continuous-time system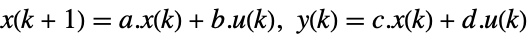
    discrete-time system
  • The descriptor state-space model ssm can be given as StateSpaceModel[{a,b,c,d,e}] in either continuous time or discrete time:
  • continuous-time system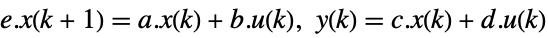
    discrete-time system
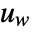  • The inputs can include the process noise as well as deterministic inputs .
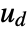  • The argument dinputs is a list of integers specifying the positions of in .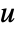
  • The outputs 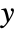consist of the noisy measurements 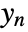as well as other outputs.
  • The argument sensors is a list of integers specifying the positions of 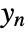in .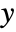
  • The arguments sensors and dinputs can also accept values All and None.
  • KalmanEstimator[ssm,{…}] is equivalent to KalmanEstimator[{ssm,All,None},{…}].
  • The noisy measurements are modeled as 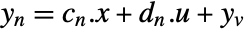, where 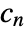and 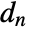are the submatrices of 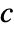and 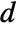associated with 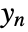, and 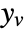is the noise.
  • The process and measurement noises are assumed to be white and Gaussian:
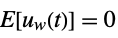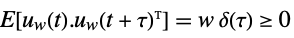
  • , process noise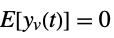
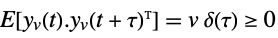
    , measurement noise
  • The cross-covariance between the process and measurement noises is given by .
  • By default, the cross-covariance matrix 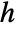is assumed to be a zero matrix.
  • KalmanEstimator supports a Method option. The following explicit settings can be given:
  • "CurrentEstimator"constructs the current estimator
    "PredictionEstimator"constructs the prediction estimator
  • The current estimate is based on measurements up to the current instant.
  • The prediction estimate is based on measurements up to the previous instant.
  • For continuous-time systems, the current and prediction estimators are the same, and the estimator dynamics are given by .
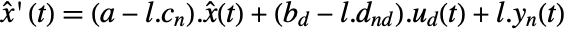  • The optimal gain for continuous-time systems is computed as l=x_r.c_n.TemplateBox[{r}, Inverse], where 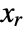solves the continuous algebraic Riccati equation a.x_r+x_r.a-x_r.c_n.TemplateBox[{r}, Inverse].c_n.x_r+b_w.q.b_w=0.
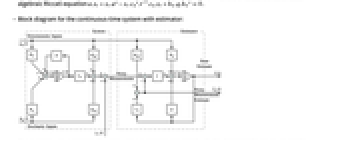
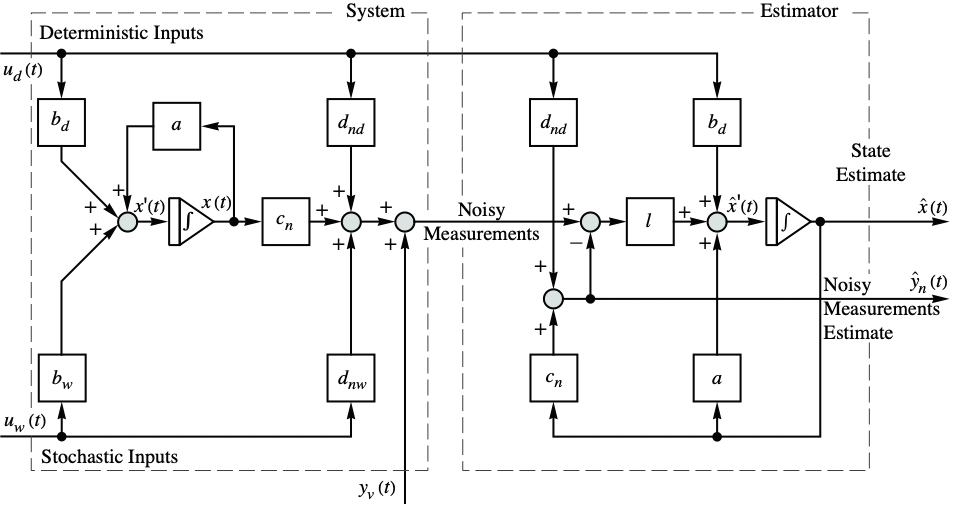
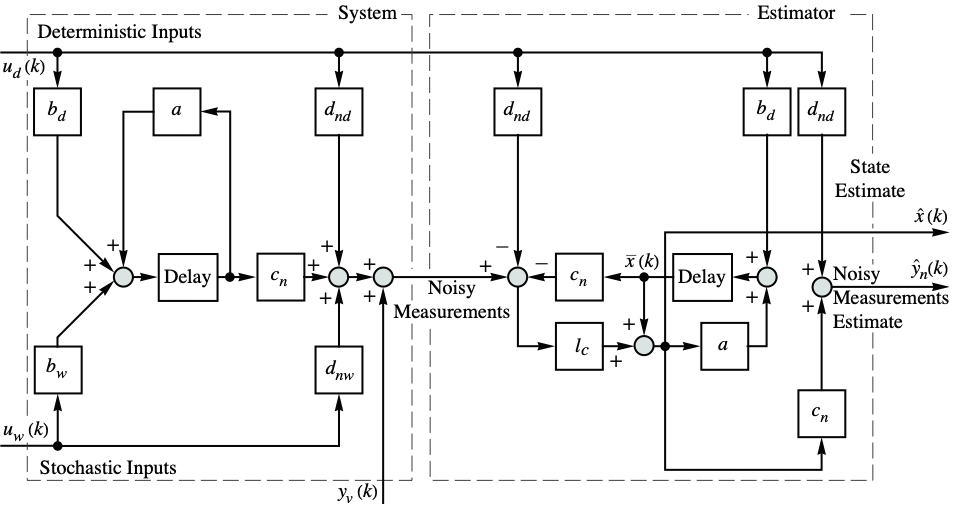
  • Block diagram for the continuous-time system with estimator:
  • The matrices with subscripts 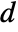, , 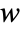and 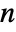are submatrices associated with the deterministic inputs, stochastic inputs, and noisy measurements, respectively.
  • For discrete-time systems, the prediction estimator dynamics are given by 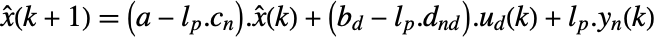. The block diagram of the discrete-time system with prediction estimator is the same as the one above.
  • The estimator dynamics of a current estimator for a discrete-time system are , and the current state estimate 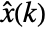is obtained from the current measurement 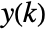as .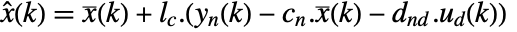
  • The optimal gain of the current estimator for a discrete-time system is computed as l_c=(x_r.c_n+b_w.h).TemplateBox[{{(, {{{c, _, n}, ., {x, _, r}, ., {{c, _, n}, }}, +, {{c, _, n}, ., {b, _, w}, ., h}, +, {{h, }, ., {{b, _, w}, }, ., {{c, _, n}, }}, +, v}, )}}, Inverse], where 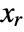solves the discrete algebraic Riccati equation .
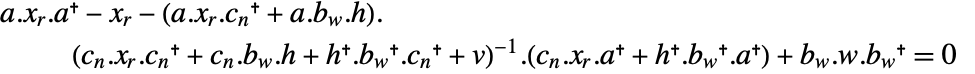  • The optimal gain 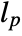of the prediction estimator for a discrete-time system is computed as .
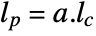  • Block diagram for the discrete-time system with current estimator:
  • The inputs to the Kalman estimator model are the deterministic inputs and the noisy measurements .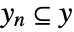
  • The outputs of the Kalman estimator model consist of the estimated states 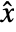and estimates of the noisy measurements .
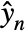  • The optimal estimator is asymptotically stable if 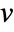is nonsingular, the pair 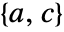is detectable, and 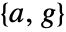is stabilizable for any .

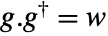Examples

open allclose all

Basic Examples  (3)

The Kalman estimator for a continuous-time system:

The Kalman estimator of a system with one stochastic output:

A discrete‐time Kalman estimator:

Scope  (5)

The Kalman estimator for a system with one measured output and one stochastic input:

The Kalman estimator of a system with nonzero cross-covariance:

The estimator for a system with one sensor output and two deterministic inputs:

The Kalman estimator for a continuous-time system with cross-correlated noise:

Find the optimal estimator for a descriptor state-space model:

Options  (2)

Method  (2)

By default, the Kalman estimator is based on the current measurements:

The prediction estimator:

For continuous-time systems, the current and prediction estimates are equivalent:

Applications  (2)

Construct a Kalman filter that smooths the response of a stochastic system:

The response of the system to a sinusoid input in the presence of process and measurement noise:

The filtered response :

A descriptor system with noise matrices:

Create Gaussian noise sequences:

Interpolate the sequences to get noise signals:

Find the system output and noisy measurement:

Design a Kalman filter:

Filter the noisy output:

Compare the actual output, measured output, and filtered output:

Properties & Relations  (2)

KalmanEstimator estimates the states and outputs of a system:

Extract the state estimator:

The output estimator:

Construct a Kalman estimator using StateOutputEstimator :

Use KalmanEstimator directly:

Wolfram Research (2010), KalmanEstimator, Wolfram Language function, https://reference.wolfram.com/language/ref/KalmanEstimator.html (updated 2012).

Text

Wolfram Research (2010), KalmanEstimator, Wolfram Language function, https://reference.wolfram.com/language/ref/KalmanEstimator.html (updated 2012).

CMS

Wolfram Language. 2010. "KalmanEstimator." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2012. https://reference.wolfram.com/language/ref/KalmanEstimator.html.

APA

Wolfram Language. (2010). KalmanEstimator. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/KalmanEstimator.html

BibTeX

@misc{reference.wolfram_2024_kalmanestimator, author="Wolfram Research", title="{KalmanEstimator}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/KalmanEstimator.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_kalmanestimator, organization={Wolfram Research}, title={KalmanEstimator}, year={2012}, url={https://reference.wolfram.com/language/ref/KalmanEstimator.html}, note=[Accessed: 21-November-2024 ]}