EstimatorGains[ssm,{p1,p2,…,pn}]
gives the estimator gain matrix for the StateSpaceModel ssm, such that the poles of the estimator are pi.
EstimatorGains[{ssm,{out1,…}},…]
specifies the measured outputs outi to use.


EstimatorGains
EstimatorGains[ssm,{p1,p2,…,pn}]
gives the estimator gain matrix for the StateSpaceModel ssm, such that the poles of the estimator are pi.
EstimatorGains[{ssm,{out1,…}},…]
specifies the measured outputs outi to use.
Details and Options


- EstimatorGains is also known as observer gains or observer pole placement.
- The state-space model ssm can be given as StateSpaceModel[{a,b,c,d}], where a, b, c, and d represent the state, input, output, and transmission matrices in either a continuous-time or a discrete-time system:
-

continuous-time system 
discrete-time system - If ssm is observable, the eigenvalues of
 will be {p1,p2,…,pn}, where
will be {p1,p2,…,pn}, where  is the computed estimator gain matrix.
is the computed estimator gain matrix. - For a descriptor system StateSpaceModel[{a,b,c,d,e}], the number of poles that can be specified is determined by the rank of e and the observability of the system. »
- EstimatorGains also accepts nonlinear systems specified by AffineStateSpaceModel and NonlinearStateSpaceModel.
- For nonlinear systems, the operating values of state and input variables are taken into consideration, and the gains are computed based on the approximate Taylor linearization.
- EstimatorGains[{ssm,{out1,…}},…] is equivalent to EstimatorGains[ssm1,…], where ssm1SystemsModelExtract[ssm,All,{out1,…}].
- The observer dynamics are given by:
-

continuous-time system 
discrete-time system - In the case of a square nonsingular matrix
 , the state vector can be computed as
, the state vector can be computed as ![x=TemplateBox[{c}, Inverse].(y-d.u) x=TemplateBox[{c}, Inverse].(y-d.u)](Files/EstimatorGains.en/8.png) .
. - EstimatorGains accepts a Method option with settings given by:
-
Automatic automatic method selection "Ackermann" Ackermann method "KNVD" Kautsky–Nichols–Van Dooren method - The estimator gains are computed as the state feedback gains of the dual system.
Examples
open all close allBasic Examples (3)
Scope (6)
A set of gains for a SISO system:
An observer gain matrix for a two-output system:
Estimator gain matrix for a three-output system with specified measurements:
Compute the estimator gains with poles specified as the roots of a polynomial:
Determine estimator gains symbolically:
Compute the gains for an AffineStateSpaceModel:
Options (6)
Method (6)
For systems with more outputs than states, Automatic finds the gains using LinearSolve:
The Ackermann method is used by default for systems with exact values:
The Ackermann method is also used for symbolic values:
For systems with numeric values, Automatic uses the "KNVD" method:
An inexact, multiple-output state-space model and desired estimator pole locations:
Find the condition number of the observability matrix for the first input:
Find the condition number of the observability matrix for the second input:
By default, the output with the lowest condition number is chosen:
Find gains for estimation through the first output:
The KNVD method uses all available outputs to estimate the states:
Applications (2)
Construct an observer for a continuous-time system:
Simulate the system with input Sin[t] and from a random initial condition:
Compare each state and its estimate:
Construct an observer for a zero-input sampled-data system:
Compute the actual and estimated states for initial states {1,–0.75,0.5} and initial observer states {0,0,0}:
Properties & Relations (7)
StateOutputEstimator assembles an observer that estimates both the states and outputs:
The prediction estimator dynamics for a discrete-time system:
Estimator gains are the conjugate transpose of state feedback gains of the dual system:
For an observable, nonsingular descriptor system, all the estimator poles can be placed:
For a singular system that is observable, only MatrixRank[e] poles can be placed:
An impulsive system where only the slow subsystem is observable:
Possible Issues (4)
The KNVD method does not handle exact systems with fewer outputs than states:
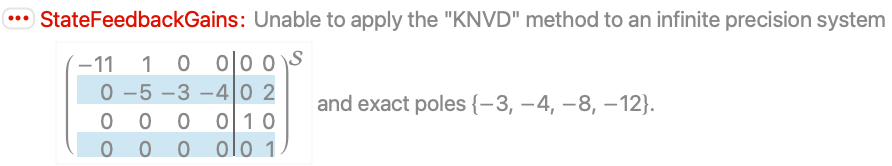
The KNVD method does not support a pole multiplicity greater than the number of outputs:
The KNVD method can give different sets of gains on different computer systems:
The observer's eigenvalues are the same:
The system must be observable:
Related Guides
History
Introduced in 2010 (8.0) | Updated in 2012 (9.0) ▪ 2014 (10.0)
Text
Wolfram Research (2010), EstimatorGains, Wolfram Language function, https://reference.wolfram.com/language/ref/EstimatorGains.html (updated 2014).
CMS
Wolfram Language. 2010. "EstimatorGains." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/EstimatorGains.html.
APA
Wolfram Language. (2010). EstimatorGains. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EstimatorGains.html
BibTeX
@misc{reference.wolfram_2025_estimatorgains, author="Wolfram Research", title="{EstimatorGains}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/EstimatorGains.html}", note=[Accessed: 08-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_estimatorgains, organization={Wolfram Research}, title={EstimatorGains}, year={2014}, url={https://reference.wolfram.com/language/ref/EstimatorGains.html}, note=[Accessed: 08-March-2026]}