Khinchin

✖
`Khinchin`

✖

Khinchin

is Khinchin's constant, with numerical value .

Details

Mathematical constant treated as numeric by NumericQ and as a constant by D.
Khinchin can be evaluated to any numerical precision using N.
Khinchin's constant (sometimes called Khintchine's constant) is given by .

Background & Context

Khinchin is the symbol representing Khinchin's constant 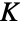, also known as Khintchine's constant. Khinchine is defined as the limiting value for the geometric mean 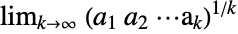of the terms 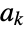of a simple continued fraction expansion of a real number 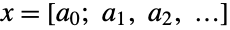, where the value of 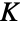is independent of the choice of 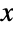. Khinchin has a numerical value 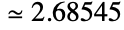and a closed form product is given by 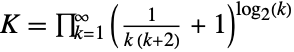. Khinchin arises most commonly in the theory of continued fractions and in ergodic theory.
When Khinchin is used as a symbol, it is propagated as an exact quantity.
It is not currently known if Khinchin is rational (meaning it can be expressed as a ratio of integers), algebraic (meaning it is the root of some integer polynomial), or normal (meaning the digits in its base- 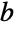expansion are equally distributed) to any base.
Khinchin can be numerically evaluated using N. However, no efficient formulas for computing large numbers of its digits are currently known. RealDigits can be used to return a list of digits of Khinchin and ContinuedFraction to obtain terms of its continued fraction expansion.

Examples

open allclose all

Basic Examples (1)Summary of the most common use cases

Evaluate to any precision:

In[1]:=1

✖

https://wolfram.com/xid/0d6jh1v1si-jdn

Out[1]=1

Scope (2)Survey of the scope of standard use cases

Do an exact numerical computation:

In[1]:=1

✖

https://wolfram.com/xid/0d6jh1v1si-y6l

Out[1]=1

TraditionalForm formatting:

In[1]:=1

✖

https://wolfram.com/xid/0d6jh1v1si-c0ija8

Applications (1)Sample problems that can be solved with this function

Geometric mean of the first 1000 continued fraction terms in π:

In[1]:=1

✖

https://wolfram.com/xid/0d6jh1v1si-p6t

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/0d6jh1v1si-qhj

Out[2]=2

Properties & Relations (2)Properties of the function, and connections to other functions

Various symbolic relations are automatically used:

In[1]:=1

✖

https://wolfram.com/xid/0d6jh1v1si

Out[1]=1

Various products give results that can be expressed using Khinchin:

In[1]:=1

✖

https://wolfram.com/xid/0d6jh1v1si

Out[1]=1

Neat Examples (1)Surprising or curious use cases

Terms in the continued fraction:

In[1]:=1

✖

https://wolfram.com/xid/0d6jh1v1si

Out[1]=1

Top