Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

LameEigenvalueA

LameEigenvalueA[ν,j,m]

给出函数 LameC[ν,j,z,m] 的第个 Lamé 本征值，其中，阶数为，为椭圆参数.

更多信息

数学函数，适宜于符号和数值运算.
连续的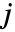的 Lamé 本征值给出 Lamé 微分方程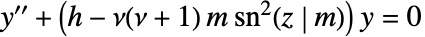（其中是 Jacobi 椭圆函数 JacobiSN[z,m]）中参数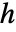的值，Lamé 微分方程的解是函数 LameC[ν,j,z,m].
对于某些特殊参数，LameEigenvalueA 自动计算出精确值.
LameEigenvalueA[ν,j,0]=j².
LameEigenvalueA 可以算出任意精度的值.
LameEigenvalueA 自动逐项作用于列表.

范例

打开所有单元关闭所有单元

基本范例 (2)

数值计算：

绘制 LameEigenvalueA 函数：

范围 (14)

数值运算 (5)

高精度运算：

输出的精度与输入的精度一致：

LameEigenvalueA 可接受复数作为参数和自变量：

在高精度条件下高效计算 LameEigenvalueA：

列表和矩阵：

特殊值 (2)

与时 LameEigenvalueA 的值：

与时 LameEigenvalueA 的值是：

对于整数值的和，LameEigenvalueA 是多项式的根：

可视化 (5)

绘制前五个 LameEigenvalueA 函数：

取复数，绘制 LameEigenvalueA 函数的绝对值：

绘制作为第一个参数的函数的 LameEigenvalueA：

绘制作为阶数和椭圆参数的函数的 LameEigenvalueA：

椭圆参数取不同的值，绘制 LameEigenvalueA 函数族：

级数展开 (1)

LameEigenvalueA 的级数展开，处有：

LameEigenvalueA 的级数展开，处有：

函数表示 (1)

TraditionalForm 格式：

应用 (1)

只有当参数的值为 LameEigenvalueA 时，LameC 才是 Lamé 微分方程的解：

属性和关系 (2)

对于整数值的和，使用 FunctionExpand 展开 LameEigenvalueA：

对于整数值的和且，LameEigenvalueA 满足对称关系：

可能存在的问题 (1)

如果为负整数，LameEigenvalueA 没有定义：

如果不是整数，LameEigenvalueA 没有定义：

顶部