LeastSquaresFilterKernel

LeastSquaresFilterKernel[{{ω1,…,ωk-1},{a1,…,ak}},n]

creates a k-band finite impulse response (FIR) filter kernel of length n designed using a least squares method, given the specified frequencies ωi and amplitudes ai.

LeastSquaresFilterKernel[{"type",spec},n]

uses the full filter specification {"type",spec}.

Details and Options

  • LeastSquaresFilterKernel returns a numeric list of length n of the impulse response coefficients of an FIR filter that has the minimum mean-squared error.
  • The impulse response of the filter is computed using the inverse discrete-time Fourier transform.
  • In LeastSquaresFilterKernel[{"type",spec},n], filter specification can be any of the following:
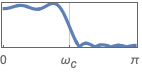
  • {"Lowpass",ωc}lowpass filter with cutoff frequency ωc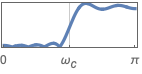
    {"Highpass",ωc}highpass filter with cutoff frequency ωc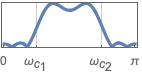
    {"Bandpass",{ωc1,ωc2}}bandpass filter with passband from ωc1 to ωc2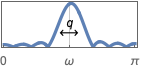
    {"Bandpass",{{ω,q}}}bandpass filter with center frequency ω and quality factor q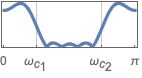
    {"Bandstop",{ωc1,ωc2}}bandstop filter with stopband from ωc1 to ωc2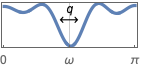
    {"Bandstop",{{ω,q}}}bandstop filter with center frequency ω and quality factor q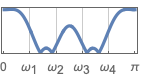
    {"Multiband",{ω1,…,ωk-1},{a1,…,ak}}multiband filter specification with k bands
    {"Differentiator",ωc}differentiator filter with cutoff frequency ωc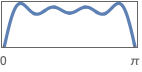
    {"Hilbert",ωc}Hilbert filter with cutoff frequency ωc
  • If "type" is omitted, "Multiband" is assumed.
  • Frequencies should be given in an ascending order such that 0≤ω1<ω2<…<ωk-1≤π.
  • Amplitude value a1 corresponds to the frequency band 0 to ω1, and amplitude ak corresponds to the frequency band ωk-1 to π.
  • Amplitude values should be non-negative. Typically, values ai=0 specify a stopband, and values ai=1 specify a passband.
  • The quality factor q is defined as 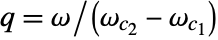, with 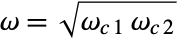being the center frequency of a bandpass or bandstop filter. Higher values of q give narrower filters.
  • The kernel ker, returned by LeastSquaresFilterKernel, can be used in ListConvolve[ker,data] to apply the filter to data.
  • LeastSquaresFilterKernel takes a WorkingPrecision option, which specifies the precision to use in internal computations. The default setting is WorkingPrecision->MachinePrecision.

Examples

open allclose all

Basic Examples  (2)

A lowpass FIR kernel:

Magnitude plot of the filter and its ideal lowpass prototype:

A Bode plot of the filter:

A multiband FIR kernel:

Magnitude plot of the filter and its "brickwall" specification:

Scope  (6)

A highpass FIR kernel:

Magnitude plot of the filter:

A bandpass FIR kernel:

Magnitude plot of the filter:

Same filter using center frequency and quality factor specification:

A bandstop FIR kernel:

Magnitude plot of the filter:

Same filter using center frequency and quality factor specification:

A differentiator FIR kernel:

Magnitude plot of the filter:

A full-band Hilbert FIR kernel:

Magnitude plot of the filter:

Plot of the imaginary part of the filter:

A half-band lowpass FIR kernel:

Magnitude plot of the filter and the half-band frequency :

Convert the half-band lowpass filter to highpass:

Magnitude plots of the two half-band filters:

Generalizations & Extensions  (1)

Improve stopband attenuation by using a Blackman window:

Applications  (4)

Create a lowpass FIR filter with cutoff frequency of and length n=15:

Taper the filter using a Blackman window to improve stopband attenuation:

Normalize:

Log-magnitude plot of the power spectra of the two filters:

Triple the length of the filter to match the bandwidth of the non-windowed sequence:

Lowpass filtering of a dual-tone multi-frequency (DTMF) signal:

This shows the spectrum of the dual-tone signal:

Create a windowed lowpass filter kernel with a cutoff frequency of 953 Hz for a sound sampled at 8000 Hz:

Here is the spectrum of the filtered signal:

Create a list of Nyquist filters:

Take a derivative of the rows of an image:

Properties & Relations  (3)

Specifying the list of frequencies and amplitudes creates a multiband filter kernel:

Increasing quality factors leads to narrower filters:

In a half-band filter of length , coefficients at positions for positive integer values of are zero:

In a -band filter, coefficients at positions are zero:

Interactive Examples  (1)

Build an audio equalizer:

Wolfram Research (2012), LeastSquaresFilterKernel, Wolfram Language function, https://reference.wolfram.com/language/ref/LeastSquaresFilterKernel.html (updated 2015).

Text

Wolfram Research (2012), LeastSquaresFilterKernel, Wolfram Language function, https://reference.wolfram.com/language/ref/LeastSquaresFilterKernel.html (updated 2015).

CMS

Wolfram Language. 2012. "LeastSquaresFilterKernel." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/LeastSquaresFilterKernel.html.

APA

Wolfram Language. (2012). LeastSquaresFilterKernel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LeastSquaresFilterKernel.html

BibTeX

@misc{reference.wolfram_2024_leastsquaresfilterkernel, author="Wolfram Research", title="{LeastSquaresFilterKernel}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/LeastSquaresFilterKernel.html}", note=[Accessed: 18-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_leastsquaresfilterkernel, organization={Wolfram Research}, title={LeastSquaresFilterKernel}, year={2015}, url={https://reference.wolfram.com/language/ref/LeastSquaresFilterKernel.html}, note=[Accessed: 18-December-2024 ]}