LeastSquaresFilterKernel
LeastSquaresFilterKernel[{{ω1,…,ωk-1},{a1,…,ak}},n]
指定された周波数が ωiで振幅が aiの場合に,最小二乗法を使って設計された,長さ n の k バンド有限インパルス応答(FIR)フィルタカーネルを作る.
LeastSquaresFilterKernel[{"type",spec},n]
完全なフィルタ指定{"type",spec}を使う.
詳細とオプション


- LeastSquaresFilterKernelは最小平均二乗誤差を持つFIRフィルタのインパルス応答係数の長さ n の数値リストを返す.
- フィルタのインパルス応答は逆離散時間フーリエ(Fourier)変換を使って計算される.
- LeastSquaresFilterKernel[{"type",spec},n]では,フィルタ指定は次の任意の形で行うことができる.
-
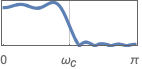
{"Lowpass",ωc} カットオフ周波数が ωcのローパスフィルタ 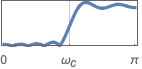
{"Highpass",ωc} カットオフ周波数が ωcのハイパスフィルタ 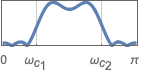
{"Bandpass",{ωc1,ωc2}} パスバンドが ωc1から ωc2までのバンドパスフィルタ 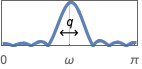
{"Bandpass",{{ω,q}}} 中心周波数 ω,Q値 q のバンドパスフィルタ 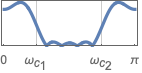
{"Bandstop",{ωc1,ωc2}} ストップバンドが ωc1から ωc2までのバンドストップフィルタ 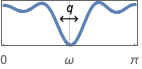
{"Bandstop",{{ω,q}}} 中心周波数 ω,Q値 q のバンドストップフィルタ 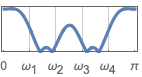
{"Multiband",{ω1,…,ωk-1},{a1,…,ak}} k バンドの多重バンドフィルタ指定 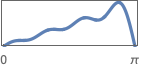
{"Differentiator",ωc} カットオフ周波数が ωcの微分器フィルタ 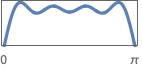
{"Hilbert",ωc} カットオフ周波数が ωcのヒルベルト(Hilbert)フィルタ - "type"が省略された場合は"Multiband"であるとみなされる.
- 周波数は0≤ω1<ω2<…<ωk-1≤π となる昇順で与えられなければならない.
- 振幅の値 a1は0から ω1までの周波数帯に相当し,振幅 akは ωk-1から π までの振幅帯に相当する.
- 振幅の値は非負でなければならない.通常,値 ai=0でストップバンドを,ai=1でパスバンドを指定する.
- Q値 q は
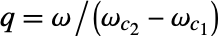 として定義される.
として定義される.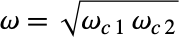 はバンドパスフィルタあるいはバンドストップフィルタの中心周波数である.q の値が大きいとフィルタは狭くなる.
はバンドパスフィルタあるいはバンドストップフィルタの中心周波数である.q の値が大きいとフィルタは狭くなる. - LeastSquaresFilterKernelによって返されたカーネル ker を ListConvolve[ker,data]で使ってフィルタを data に適用することができる.
- LeastSquaresFilterKernelは内部計算精度を指定するWorkingPrecisionオプションを取る.デフォルト設定はWorkingPrecision->MachinePrecisionである.
例題
すべて開くすべて閉じるテキスト
Wolfram Research (2012), LeastSquaresFilterKernel, Wolfram言語関数, https://reference.wolfram.com/language/ref/LeastSquaresFilterKernel.html (2015年に更新).
CMS
Wolfram Language. 2012. "LeastSquaresFilterKernel." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/LeastSquaresFilterKernel.html.
APA
Wolfram Language. (2012). LeastSquaresFilterKernel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LeastSquaresFilterKernel.html