LeastSquaresFilterKernel[{{ω1,…,ωk-1},{a1,…,ak}},n]
使用一个使用最小二乘法设计的长度为 n 的 k 个频带的有限脉冲响应 (FIR) 滤波器,给定指定频率 ωi 和幅值 ai.
LeastSquaresFilterKernel[{"type",spec},n]
使用全滤波器指标 {"type",spec}.


LeastSquaresFilterKernel
LeastSquaresFilterKernel[{{ω1,…,ωk-1},{a1,…,ak}},n]
使用一个使用最小二乘法设计的长度为 n 的 k 个频带的有限脉冲响应 (FIR) 滤波器,给定指定频率 ωi 和幅值 ai.
LeastSquaresFilterKernel[{"type",spec},n]
使用全滤波器指标 {"type",spec}.
更多信息和选项


- LeastSquaresFilterKernel 对具有最小均方差的 FIR 滤波器的脉冲响应系数,返回长度为 n 的数值列表.
- 滤波器的脉冲响应使用离散时间傅里叶逆变换计算.
- 在 LeastSquaresFilterKernel[{"type",spec},n] 中,滤波器指标可以为下面任何之一:
-
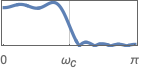
{"Lowpass",ωc} 截止频率为 ωc 的低通滤波器 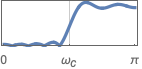
{"Highpass",ωc} 截止频率为 ωc 的高通滤波器 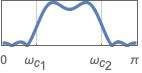
{"Bandpass",{ωc1,ωc2}} 通带从 ωc1 到 ωc2 的带通滤波器 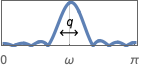
{"Bandpass",{{ω,q}}} 中心频率为 ω 和质量因子为 q 的带通滤波器 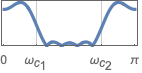
{"Bandstop",{ωc1,ωc2}} 阻带从 ωc1 到 ωc2 的带阻滤波器 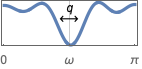
{"Bandstop",{{ω,q}}} 中心频率为 ω 和质量因子为 q 的带阻滤波器 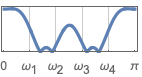
{"Multiband",{ω1,…,ωk-1},{a1,…,ak}} 有 k 个频带的多带滤波器规范 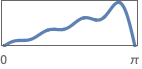
{"Differentiator",ωc} 截止频率为 ωc 的微分滤波器 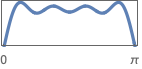
{"Hilbert",ωc} 截止频率为 ωc 的 Hilbert 滤波器 - 如果忽略 "type",则假定采用 "Multiband".
- 频率应该以升序给出,以满足 0≤ω1<ω2<…<ωk-1≤π.
- 幅值 a1 对应于从 0 到 ω1 的频带,而幅值 ak 对应于从 ωk-1 到 π 的频带.
- 幅值应该是非负的. 通常情况下,数值 ai=0 指定一个阻带,而数值 ai=1 指定一个通带.
- 质量因子 q 定义为
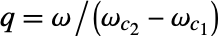 ,其中
,其中 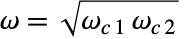 是带通或者带阻滤波器的中心频率. q 的值越大,给出的滤波器越窄.
是带通或者带阻滤波器的中心频率. q 的值越大,给出的滤波器越窄. - 可将由 LeastSquaresFilterKernel 返回的核 ker 用于 ListConvolve[ker,data] 中,来对 data 进行滤波.
- 可给出以下选项:
-
WorkingPrecision MachinePrecision 内部计算使用的精度
范例
打开所有单元 关闭所有单元范围 (6)
应用 (4)
相关指南
-
▪
- 信号滤波与滤波器设计 ▪
- 信号处理
文本
Wolfram Research (2012),LeastSquaresFilterKernel,Wolfram 语言函数,https://reference.wolfram.com/language/ref/LeastSquaresFilterKernel.html (更新于 2015 年).
CMS
Wolfram 语言. 2012. "LeastSquaresFilterKernel." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2015. https://reference.wolfram.com/language/ref/LeastSquaresFilterKernel.html.
APA
Wolfram 语言. (2012). LeastSquaresFilterKernel. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/LeastSquaresFilterKernel.html 年
BibTeX
@misc{reference.wolfram_2025_leastsquaresfilterkernel, author="Wolfram Research", title="{LeastSquaresFilterKernel}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/LeastSquaresFilterKernel.html}", note=[Accessed: 03-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_leastsquaresfilterkernel, organization={Wolfram Research}, title={LeastSquaresFilterKernel}, year={2015}, url={https://reference.wolfram.com/language/ref/LeastSquaresFilterKernel.html}, note=[Accessed: 03-February-2026]}