WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

LinearProgramming

LinearProgrammingはバージョン13.0でLinearOptimizationに置き換えられた．

LinearProgramming[c,m,b]

m.x≥b および x≥0の制約条件の下で，量 c.x を最小にするベクトル x を求める．

LinearProgramming[c,m,{{b₁,s₁},{b₂,s₂},…}]

x≥0であり，行列 m と{b_i,s_i}のペアによって指定される線形制約条件の下で c.x を最小にするベクトル x を求める．m の各行 m_i の対応する条件は，s_i==1の場合は m_i.x≥b_i，s_i==0の場合は m_i.x==b_i，s_i==-1の場合は m_i.x≤b_i である．

LinearProgramming[c,m,b,l]

m，b，および x≥l によって指定される制約条件の下で c.x を最小にする．

LinearProgramming[c,m,b,{l₁,l₂,…}]

m，b，および x_i≥l_i によって指定される制約条件の下で c.x を最小にする．

LinearProgramming[c,m,b,{{l₁,u₁},{l₂,u₂},…}]

m，b，および l_i≤x_i≤u_i によって指定される制約条件の下で c.x を最小にする．

LinearProgramming[c,m,b,lu,dom]

x の要素が，RealsかIntegersのどちらかの領域 dom にあるものとする．

LinearProgramming[c,m,b,lu,{dom₁,dom₂,…}]

x_i が領域 dom_i にあるものとする．

詳細とオプション

ベクトル c と b そして行列 m のすべての要素が実数であることが要求される．
境界 l_iと u_iは，実数，Infinityまたは-Infinityでなければならない．
Noneは境界を指定しないことに等しい．
LinearProgrammingは，入力が厳密な有理数である場合は，厳密な有理数または整数の結果を返す．
解が求められないときは，LinearProgrammingは未評価で返される．
入力に近似数が含まれるとき，LinearProgrammingは近似数値解を出す．オプションToleranceは内部比較で使用する許容率を指定する．デフォルト値はTolerance->Automaticである．これは厳密数には厳密な比較を行い，近似数には許容率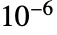を使う．
LinearProgrammingでSparseArrayオブジェクトを使うことができる．
Method->"InteriorPoint"とすると，LinearProgrammingは内点法を使う．

例題

すべて開くすべて閉じる

例 (3)

と暗示的な非負という条件下でを最小化する：

LinearProgrammingはLinearOptimizationに置き換えられた：

方程式の制約条件と暗示的な非負という制約条件下で問題を解く：

LinearOptimizationを使って問題を解く：

方程式の制約条件と暗示的な非負という制約条件下で問題を解く：

LinearOptimizationを使って問題を解く：

スコープ (6)

と下界 , という制約条件に従ってを最小化する：

と下界, という制約条件に従ってを最小化する：

と上界 , という制約条件に従ってを最小化する：

と暗示的な非負という制約条件に従ってを最小化する：

とという境界条件のみでを最小化する：

両変数を整数として同様の問題を解く：

最初の変数を整数として同じ問題を解く：

より規模の大きいLP．この場合は変数が200,000個で制約条件が10,000個のものを解く：

オプション (2)

Method (1)

"InteriorPoint"は，機械精度の問題でしか使えないが，"Simplex"や"RevisedSimplex"より速い：

Tolerance (1)

近似的な解で十分な場合は，ルーズなToleranceオプションを使って解の処理を速めることができる：

特性と関係 (2)

線形計画法問題はMinimizeを使って解くこともできる：

NMinimizeまたはFindMinimumを使って厳密ではない線形計画法の問題を解いてもよい：

考えられる問題 (4)

整数計画法のアルゴリズムは機械数の問題でしか使えない：

"InteriorPoint"（内点）法は機械数にしか使えない：

"InteriorPoint"法は最適解群の中央の解を返すことがある：

"InteriorPoint"（シンプレックス）法は，常に最適解の角の解を返す：

この場合，最適解群はからまでの線分上のすべての点である：

"InteriorPoint"法は，問題が実行不可能かあるいは境界を持たないかどうかを常に見分けられる訳ではない：

おもしろい例題 (1)

次は，次元のKlee–Minty問題をLinearProgramming構文で表している：

スケーリングが内部的に適用されているので，シンプレックス法は非常に速く収束する：

トップへ