LinearProgramming
LinearProgramming[c,m,b]
求向量 x,使 c.x 在约束条件 m.x≥b 和 x≥0 下达到极小.
LinearProgramming[c,m,{{b1,s1},{b2,s2},…}]
求向量 x,使 c.x 在 x≥0 和由矩阵 m 和 {bi,si} 确定的约束下达到最小. 对于 m 的每个行 mi,如果 si==1,则相应的约束是 mi.x≥bi,如果 si==0,则为 mi.x==bi,如果 si==-1,为 mi.x≤bi.
LinearProgramming[c,m,b,l]
在由 m、b 和 x≥l 确定的约束下最小化 c.x.
LinearProgramming[c,m,b,{l1,l2,…}]
在由 m、b 和 xi≥li 确定的约束下最小化 c.x.
LinearProgramming[c,m,b,{{l1,u1},{l2,u2},…}]
在由 m、b 和 li≤xi≤ui 确定的约束下最小化 c.x.
LinearProgramming[c,m,b,lu,{dom1,dom2,…}]
xi 位于域 domi 内.
更多信息和选项

- 在向量 c 和 b 及矩阵 m 的所有分量必须是数.
- 边界值 li 和 ui 必须是实数或 Infinity 或 -Infinity.
- None 等于没有边界.
- 如果 LinearProgramming 的输入包含明确的有理数,它给出明确的有理数结果或整数结果.
- 如果没有找到任何解,LinearProgramming 返回不计算的形式:
- 如果 LinearProgramming 的输入包含近似数,它给出近似数的结果. 选项 Tolerance 指定内部比较使用的误差. 缺省是 Tolerance->Automatic,它对精确数执行比较,对近似数使用误差
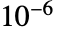 .
. - SparseArray 对象可以用于 LinearProgramming.
- 设置 Method->"InteriorPoint",LinearProgramming 用内点法.
范例
打开所有单元关闭所有单元基本范例 (3)
范围 (6)
选项 (2)
Tolerance (1)
如果近似解足够满足条件,取消选项 Tolerance 会使求解速度更快:
属性和关系 (2)
可能存在的问题 (4)
文本
Wolfram Research (1991),LinearProgramming,Wolfram 语言函数,https://reference.wolfram.com/language/ref/LinearProgramming.html (更新于 2007 年).
CMS
Wolfram 语言. 1991. "LinearProgramming." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2007. https://reference.wolfram.com/language/ref/LinearProgramming.html.
APA
Wolfram 语言. (1991). LinearProgramming. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/LinearProgramming.html 年