ListFourierSequenceTransform
ListFourierSequenceTransform[list,ω]
リストの離散時間フーリエ変換(DTFT)をパラメータ ω の関数として与える.
ListFourierSequenceTransform[list,ω,k]
整数時間 k における list の第1要素を無限時間軸上に置く.
ListFourierSequenceTransform[list,{ω1,ω2,…},{k1,k2,…}]
多次元離散時間フーリエ変換を与える.
詳細とオプション

- デフォルトで,長さ
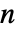 のリスト
のリスト 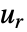 の一次元離散時間フーリエ変換は,
の一次元離散時間フーリエ変換は,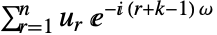 として計算される.
として計算される. - ListFourierSequenceTransform[list,ω]はListFourierSequenceTransform[list,ω,0]に等しい.
- ListFourierSequenceTransformは,FourierParametersオプションを取る.次は,FourierParametersのよく使われる設定値である.
-
{1,1} 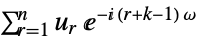
デフォルト設定 {1,-2Pi} 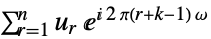
周期1 {a,b} 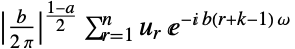
一般的な設定 - ListFourierSequenceTransform[list,ω,k]は,事実上,数列 f について,1<=r<=Length[list]の場合は f[r-1+k]=list[[r]],その他の場合は f[r]=0としてFourierSequenceTransform[f[r],r,ω]を計算する.
例題
すべて開くすべて閉じる特性と関係 (4)
数値リストの離散時間フーリエ変換は,シフトされた単位サンプルの総和のフーリエ数列変換に等しい:
長さ ![]() のリストのFourierは,
のリストのFourierは,![]() の倍数に当る周波数でのListFourierSequenceTransformのサンプルを返す:
の倍数に当る周波数でのListFourierSequenceTransformのサンプルを返す:
ListFourierSequenceTransformはListZTransformを単位円上で計算することに等しい:
テキスト
Wolfram Research (2012), ListFourierSequenceTransform, Wolfram言語関数, https://reference.wolfram.com/language/ref/ListFourierSequenceTransform.html.
CMS
Wolfram Language. 2012. "ListFourierSequenceTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ListFourierSequenceTransform.html.
APA
Wolfram Language. (2012). ListFourierSequenceTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ListFourierSequenceTransform.html