WOLFRAM

Wolfram Language & System Documentation Center

MandelbrotSetMemberQ[z]

returns True if z is in the Mandelbrot set, and False otherwise.

Details and Options
Details and Options Details and Options
Examples  
Basic Examples  
Scope  
Options  
MaxIterations  
Applications  
Possible Issues  
Neat Examples  
See Also
Related Guides
History
Cite this Page

MandelbrotSetMemberQ

MandelbrotSetMemberQ[z]

returns True if z is in the Mandelbrot set, and False otherwise.

Details and Options

  • The Mandelbrot set is the set of all complex numbers 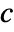for which the sequence 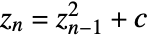does not diverge to infinity when starting with .
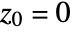  • With the option MaxIterations->n, the sequence 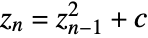will be iterated at most n times to determine if the sequence diverges.
  • The default setting is MaxIterations->1000.
  • If the maximum number of iterations is reached, z is assumed to be in the Mandelbrot set.

Examples

open all close all

Basic Examples  (3)

Test whether is a member of the Mandelbrot set:

Zero is known to be inside the Mandelbrot set:

It takes a few hundred iterations to determine that 0.2501 is not in the Mandelbrot set:

Scope  (2)

MandelbrotSetMemberQ threads itself element-wise over lists:

MandelbrotSetMemberQ works on all kinds of numbers:

Options  (1)

MaxIterations  (1)

Sometimes MaxIterations needs to be increased to eliminate false positives:

Applications  (2)

Generate the Mandelbrot set from randomly chosen points:

Approximate the first point along the line that is not in the Mandelbrot set:

Show the point on the Mandelbrot set:

Possible Issues  (1)

With MaxIterations->Infinity, the calculation may not converge in a finite number of steps:

Neat Examples  (4)

MandelbrotSetMemberQ can be used to get an estimate of the area of the Mandelbrot set:

Display the Julia sets for points in the Mandelbrot set:

Rotate the Mandelbrot set:

Use MandelbrotSetMemberQ to distinguish Julia sets that are Cantor sets:

Wolfram Research (2014), MandelbrotSetMemberQ, Wolfram Language function, https://reference.wolfram.com/language/ref/MandelbrotSetMemberQ.html.

Text

Wolfram Research (2014), MandelbrotSetMemberQ, Wolfram Language function, https://reference.wolfram.com/language/ref/MandelbrotSetMemberQ.html.

CMS

Wolfram Language. 2014. "MandelbrotSetMemberQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MandelbrotSetMemberQ.html.

APA

Wolfram Language. (2014). MandelbrotSetMemberQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MandelbrotSetMemberQ.html

BibTeX

@misc{reference.wolfram_2025_mandelbrotsetmemberq, author="Wolfram Research", title="{MandelbrotSetMemberQ}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/MandelbrotSetMemberQ.html}", note=[Accessed: 30-October-2025]}

BibLaTeX

@online{reference.wolfram_2025_mandelbrotsetmemberq, organization={Wolfram Research}, title={MandelbrotSetMemberQ}, year={2014}, url={https://reference.wolfram.com/language/ref/MandelbrotSetMemberQ.html}, note=[Accessed: 30-October-2025]}