MandelbrotSetPlot[{zmin,zmax}]
plots the portion of the Mandelbrot set inside the rectangle with corners zmin and zmax.
plots the Mandelbrot set over a default rectangle.




MandelbrotSetPlot
MandelbrotSetPlot[{zmin,zmax}]
plots the portion of the Mandelbrot set inside the rectangle with corners zmin and zmax.
plots the Mandelbrot set over a default rectangle.
Details and Options

- The Mandelbrot set is the set of all complex numbers c for which the sequence
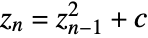 does not diverge to infinity when starting with
does not diverge to infinity when starting with 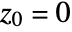 .
. - The default rectangle for MandelbrotSetPlot[] has corners
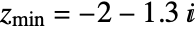 and
and 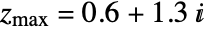 .
. - MandelbrotSetPlot produces a Graphics object containing a Raster primitive.
- MandelbrotSetPlot[] has the same options as Graphics, with the following additions:
-
ColorFunction Automatic how to determine the color of a pixel EscapeRadius 2 how to determine that a point is not in the set Frame True whether to draw a frame around the plot ImageResolution 500 resolution of the image in the larger direction MaxIterations 1000 maximum number of iterates per point PerformanceGoal $PerformanceGoal aspects of performance to try to optimize PlotLegends None legends for the number of interactions PlotTheme $PlotTheme overall theme for the plot - With MaxIterations->n, where n is a positive integer, the function
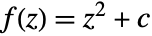 will be iterated at most n times to determine if the orbit of 0 ever exceeds 2.
will be iterated at most n times to determine if the orbit of 0 ever exceeds 2. - With ColorFunction->f, where f is a function, the argument of f is a real number in
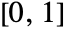 proportional to the number of iterates, and f must return color directives, such as RGBColor and Hue, or named colors, such as Red and Blue.
proportional to the number of iterates, and f must return color directives, such as RGBColor and Hue, or named colors, such as Red and Blue. - ColorFunction->"name" is equivalent to ColorFunction->(If[#1,Black,ColorData["name"][#]]&).
- The list of possible color function names is given by ColorData["Gradients"].
Examples
open all close allBasic Examples (3)
Options (59)
AspectRatio (4)
By default, MandelbrotSetPlot uses the same width and height:
Use numerical value to specify the height-to-width ratio:
AspectRatioAutomatic determines the ratio from the plot ranges:
AspectRatioFull adjusts the height and width to tightly fit inside other constructs:
Axes (3)
By default, MandelbrotSetPlot uses a frame instead of axes:
AxesOrigin (2)
AxesStyle (4)
ColorFunction (5)
Frame (3)
FrameLabel (4)
FrameTicks (8)
Use frame ticks on the bottom edge:
By default, the top and right edges have tick marks but no tick labels:
Use All to include tick labels on all edges:
Place tick marks at specific positions:
Draw frame tick marks at specified positions with specific labels:
Specify the lengths for tick marks as a fraction of the graphics size:
Use different sizes in the positive and negative directions for each tick mark:
Specify a style for each frame tick:
Construct a function that places frame ticks at the midpoint and extremes of the frame edge:
ImageResolution (1)
Increase ImageResolution for finer plots:
ImageSize (7)
Use named sizes such as Tiny, Small, Medium and Large:
Specify the width of the plot:
Specify the height of the plot:
Allow the width and height to be up to a certain size:
Specify the width and height for a graphic, padding with space if necessary:
Setting AspectRatioFull will fill the available space:
Use maximum sizes for the width and height:
Use ImageSizeFull to fill the available space in an object:
Specify the image size as a fraction of the available space:
MaxIterations (1)
Increase MaxIterations to improve quality when zooming in:
Ticks (4)
Properties & Relations (3)
Points in the Mandelbrot set determine quadratic Julia sets:
Use MandelbrotSetMemberQ to determine whether a point is in the Mandelbrot set:
MandelbrotSetIterationCount gives the number of iterations used to determine if a point is not in the Mandelbrot set:
See Also
JuliaSetPlot MandelbrotSetIterationCount MandelbrotSetMemberQ MandelbrotSetBoettcher ArrayPlot DensityPlot ContourPlot
Function Repository: MandelbrotSetRemap
Related Guides
History
Text
Wolfram Research (2014), MandelbrotSetPlot, Wolfram Language function, https://reference.wolfram.com/language/ref/MandelbrotSetPlot.html.
CMS
Wolfram Language. 2014. "MandelbrotSetPlot." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MandelbrotSetPlot.html.
APA
Wolfram Language. (2014). MandelbrotSetPlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MandelbrotSetPlot.html
BibTeX
@misc{reference.wolfram_2025_mandelbrotsetplot, author="Wolfram Research", title="{MandelbrotSetPlot}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/MandelbrotSetPlot.html}", note=[Accessed: 10-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_mandelbrotsetplot, organization={Wolfram Research}, title={MandelbrotSetPlot}, year={2014}, url={https://reference.wolfram.com/language/ref/MandelbrotSetPlot.html}, note=[Accessed: 10-March-2026]}