

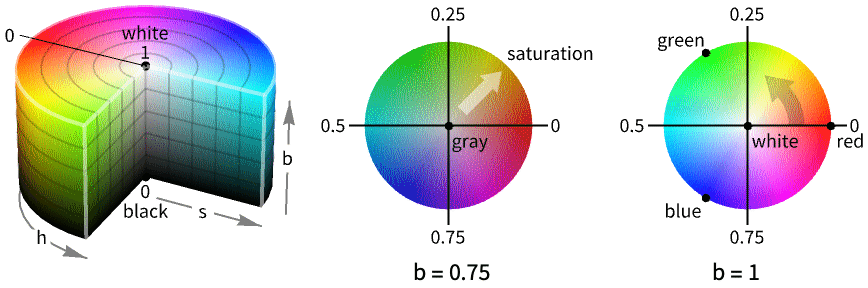
Hue
Details


- Hue is also known as HSB (hue, saturation and brightness) or HSV (hue, saturation and value).
- Hue corresponds to a cylindrical transformation of RGBColor, typically used for color picking, allowing for easier interpretation of color parameters.
- The parameters h, s, b, and a must all be between 0 and 1. Values of s, b, and a outside this range are clipped. Values of h outside this range are treated cyclically. »
- As h varies from 0 to 1, the color corresponding to Hue[h] runs through red, yellow, green, cyan, blue, magenta, and back to red again. »
- Hue[color] can be used to convert any ColorQ expression to HSB.
- Hue["htmlcolor"] can be used to represent the HTML color "htmlcolor" in the HSB space.
- If no opacity has been specified, Hue[h,s,b] is equivalent to Hue[h,s,b,1].
- Hue[h,s,b,a] is equivalent to {Hue[h,s,b],Opacity[a]}.
- Hue[h] is equivalent to Hue[h,1,1]. »
- The alternative forms Hue[{h,s,b}] and Hue[{h,s,b,a}] can also be used. »
- On monochrome output devices, a gray level based on the brightness value is used.
- ColorConvert can be used to convert Hue to other color spaces.
- The following wrappers can be used around colors:
-
ColorsNear[color,…] specifies a region around color Directive[…,color,…] specifies a color in combination with other directives Glow[color] specifies color independent of lighting » Opacity[a,color] specifies a color with an opacity a Style[expr,color] displays expr with the specified color » - For 3D surfaces, explicit Hue directives define surface colors; the final shading depends on lighting.
Examples
open all close allBasic Examples (4)
Scope (3)
Generalizations & Extensions (3)
Applications (8)
Visualization (3)
HSB Color Model (5)
Plot the iso hue surfaces from the RGB cube. The hues are 0 (red), 1/6 (yellow), 2/6 (green), 3/6 (cyan), 4/6 (blue), and 5/6 (magenta). The primary colors are red at 0, green at 1/3, and blue at 2/3. The secondary colors are mixtures of two primary colors, so yellow at 1/6 is a mixture of equal parts red and green, etc.:
Manipulating the hue component interactively makes this easier to understand:
Plot the iso saturation surfaces from the RGB cube. The resulting iso surfaces are hexagonal cones, and the HSB color model is also known as the hexcone model:
Saturation for RGBColor[r,g,b] is given by (Max[r,g,b]-Min[r,g,b])/Max[r,g,b], so saturation 0 corresponds to the gray line, i.e. ![]() :
:
Saturation 1 corresponds (see above) to the surfaces ![]() ,
, ![]() , or
, or ![]() :
:
Manipulating the iso saturation surfaces makes it more intuitive:
Plot the iso brightness surfaces. The brightness for RGBColor[r,g,b] is given by Max[r,g,b], maximal output from any color channel:
Brightness 0 corresponds to black, i.e. RGBColor[0,0,0]:
Brightness 1 corresponds to the planes ![]() ,
, ![]() , or
, or ![]() :
:
Manipulating the iso brightness surfaces makes it more intuitive:
Plot iso chroma or colorfulness surfaces in the RGB cube. The chroma c for Hue[h,s,b] is given by c==s b, resulting in saturation sc/b:
Chroma for RGBColor[r,g,b] is the distance to the gray point with the same brightness. The resulting formula is Max[r,g,b]-Min[r,g,b], which can also be used to visualize the following:
Chroma 0, the achromatic colors, corresponds to the gray line ![]() :
:
Manipulating the iso chroma surfaces gives more intuition:
Combine the iso saturation and iso brightness surfaces and show that the intersection is a polygonal curve. The hue is the fraction of length around this polygonal curve in the counterclockwise direction as seen from the white RGB corner, i.e. ![]() , starting at red:
, starting at red:
Iso saturation and iso brightness intersect at the hue curve, a polygonal curve with six vertices:
Properties & Relations (1)
Possible Issues (1)
Saturation and brightness values outside of the 0, 1 range will be clipped:
In plot functions, use ColorFunctionScaling to control global scaling of variables:
See Also
RGBColor GrayLevel CMYKColor Opacity Blend Lighter Darker Glow Specularity Lighting Raster Red Green Blue White ColorSlider ColorConvert ColorDistance
Function Repository: DLMFHue
Related Guides
History
Introduced in 1991 (2.0) | Updated in 2007 (6.0) ▪ 2008 (7.0) ▪ 2021 (12.3)
Text
Wolfram Research (1991), Hue, Wolfram Language function, https://reference.wolfram.com/language/ref/Hue.html (updated 2021).
CMS
Wolfram Language. 1991. "Hue." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/Hue.html.
APA
Wolfram Language. (1991). Hue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Hue.html
BibTeX
@misc{reference.wolfram_2025_hue, author="Wolfram Research", title="{Hue}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/Hue.html}", note=[Accessed: 04-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_hue, organization={Wolfram Research}, title={Hue}, year={2021}, url={https://reference.wolfram.com/language/ref/Hue.html}, note=[Accessed: 04-March-2026]}