WOLFRAM

Wolfram Language & System Documentation Center

MandelbrotSetBoettcher[z]

gives the Böttcher coordinate of z with respect to the Mandelbrot set.

Details and Options
Details and Options Details and Options
Examples  
Basic Examples  
Scope  
Options  
MaxIterations  
Applications  
Neat Examples  
See Also
Related Guides
History
Cite this Page

MandelbrotSetBoettcher

MandelbrotSetBoettcher[z]

gives the Böttcher coordinate of z with respect to the Mandelbrot set.

Details and Options

  • The Mandelbrot set is the set of all complex numbers 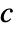for which the sequence 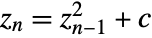does not diverge to infinity when starting with .
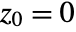  • With the option MaxIterations->m, the sequence 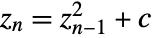will be iterated at most m times to approximate .
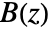  • The default setting is MaxIterations->100.
  • MandelbrotSetBoettcher can be evaluated to arbitrary numerical precision.
  • MandelbrotSetBoettcher automatically threads over lists.

Examples

open all close all

Basic Examples  (3)

Get the Böttcher coordinate of :

Since is in the Mandelbrot set, the result is undefined:

Make an asymptotic series approximation for the Böttcher function:

Scope  (3)

MandelbrotSetBoettcher threads itself element-wise over lists:

MandelbrotSetBoettcher works on all kinds of numbers:

Evaluate to high precision:

Options  (1)

MaxIterations  (1)

Sometimes MaxIterations needs to be increased:

Applications  (3)

Use the absolute value to display "equipotential lines" for the Mandelbrot set:

Use the argument to display "field lines" for the Mandelbrot set:

Use the argument to display the "external ray" with angle :

Neat Examples  (1)

Approximate the inverse to the Böttcher function and apply it to the unit circle:

Wolfram Research (2014), MandelbrotSetBoettcher, Wolfram Language function, https://reference.wolfram.com/language/ref/MandelbrotSetBoettcher.html.

Text

Wolfram Research (2014), MandelbrotSetBoettcher, Wolfram Language function, https://reference.wolfram.com/language/ref/MandelbrotSetBoettcher.html.

CMS

Wolfram Language. 2014. "MandelbrotSetBoettcher." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MandelbrotSetBoettcher.html.

APA

Wolfram Language. (2014). MandelbrotSetBoettcher. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MandelbrotSetBoettcher.html

BibTeX

@misc{reference.wolfram_2025_mandelbrotsetboettcher, author="Wolfram Research", title="{MandelbrotSetBoettcher}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/MandelbrotSetBoettcher.html}", note=[Accessed: 13-August-2025]}

BibLaTeX

@online{reference.wolfram_2025_mandelbrotsetboettcher, organization={Wolfram Research}, title={MandelbrotSetBoettcher}, year={2014}, url={https://reference.wolfram.com/language/ref/MandelbrotSetBoettcher.html}, note=[Accessed: 13-August-2025]}