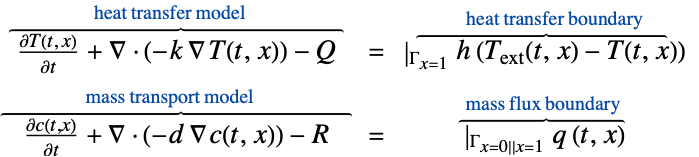MassFluxValue
MassFluxValue[pred,vars,pars]
偏微分方程式のための質量流束境界条件を,適用される場所を示す境界 pred,モデル変数 vars,大域パラメータ pars で表す.
MassFluxValue[pred,vars,pars,lkey]
質量流束境界条件を pars[lkey]で指定される局所パラメータで表す.
詳細




- MassFluxValueはMassTransportPDEComponentについての境界条件を指定し,以下のモデリング方程式の一部として使われる.
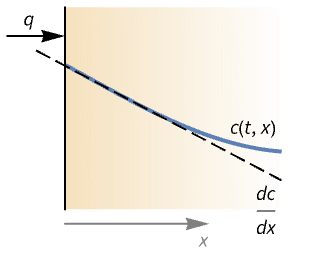
- MassFluxValueは,一般に,領域外の種源あるいシンクによって形成された,境界を通る質量種の流れをモデル化するために使われる.
- 流量は,エネルギーや質量の量の時間あたりの流れのことである.流束は境界を通る流量のことで,時間あたり面積あたりの数量の単位で計量される.1時間あたりの開口面積の断面あたりの1ミリメートルの雨が雨の流れである.
- MassFluxValueは,境界の一部を通って流入する質量種の割合を,従属変数
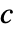 (単位:[
(単位:[![TemplateBox[{InterpretationBox[, 1], {"mol", , "/", , {"m", ^, 3}}, moles per meter cubed, {{(, "Moles", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"mol", , "/", , {"m", ^, 3}}, moles per meter cubed, {{(, "Moles", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/MassFluxValue.ja/4.png) ]),独立変数
]),独立変数 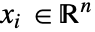 (単位:[
(単位:[![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/MassFluxValue.ja/6.png) ]),時間変数
]),時間変数 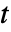 (単位:[
(単位:[![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/MassFluxValue.ja/8.png) ])でモデル化する.
])でモデル化する. - 定常変数 vars は vars={c[x1,…,xn],{x1,…,xn}}である.
- 時間依存変数 vars は vars={c[t,x1,…,xn],t,{x1,…,xn}}である.
- 非保存型時間依存物質移動モデルMassTransportPDEComponentは,質量拡散係数
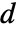 ,物質対流速度ベクトル
,物質対流速度ベクトル  ,質量反応率
,質量反応率  ,物質源項
,物質源項  の対流拡散モデルに基づいている.
の対流拡散モデルに基づいている. - 保存型時間依存物質移動モデルMassTransportPDEComponentは,以下で与えられる保存型対流拡散モデルに基づいている.
- 質量流束
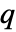 (単位:
(単位: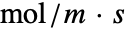 ),境界単位法線
),境界単位法線 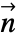 の非保存型のMassFluxValueは以下をモデル化する.
の非保存型のMassFluxValueは以下をモデル化する. - 保存型のMassFluxValueモデル
- モデルパラメータ pars はMassTransportPDEComponentについてと同じように指定できる.
- 次の追加的なモデルパラメータ pars を与えることができる.
-
パラメータ デフォルト シンボル "BoundaryUnitNormal" Automatic 
"MassFlux" - 0
 ,質量流束(単位:[
,質量流束(単位:[![TemplateBox[{InterpretationBox[, 1], {"mol", , "/(", , "m", , "s", , ")"}, moles per meter second, {{(, "Moles", )}, /, {(, {"Meters", , "Seconds"}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"mol", , "/(", , "m", , "s", , ")"}, moles per meter second, {{(, "Moles", )}, /, {(, {"Meters", , "Seconds"}, )}}}, QuantityTF]](Files/MassFluxValue.ja/23.png) ])
])"ModelForm" "NonConservative" - - モデルパラメータはどれも,
 ,
, ,
,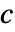 の任意のもの,あるいは他の従属変数に依存することがある.
の任意のもの,あるいは他の従属変数に依存することがある. - モデルパラメータを局所化したければ,キー lkey を指定して連想 pars[lkey]からの値をモデルパラメータに使うことができる.
- MassFluxValueを評価するとNeumannValueになる.
- 境界述語 pred はNeumannValueにおけるのと同じように指定できる.
- MassFluxValueが連想 pars で…,keypi…,pivi,…]として指定されるパラメータ
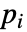 に依存するなら,パラメータ
に依存するなら,パラメータ 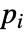 は
は 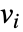 で置換される.
で置換される.

例題
すべて開くすべて閉じるスコープ (10)
基本的な例題 (2)
1D (1)
2D (1)
3D (1)
材料領域 (1)
時間依存 (1)
非線形時間依存 (1)
アプリケーション (2)
単一の方程式 (1)
Wolfram Research (2020), MassFluxValue, Wolfram言語関数, https://reference.wolfram.com/language/ref/MassFluxValue.html.
テキスト
Wolfram Research (2020), MassFluxValue, Wolfram言語関数, https://reference.wolfram.com/language/ref/MassFluxValue.html.
CMS
Wolfram Language. 2020. "MassFluxValue." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MassFluxValue.html.
APA
Wolfram Language. (2020). MassFluxValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MassFluxValue.html