MassTransferValue[pred,vars,pars]
represents a mass transfer boundary condition for PDEs with predicate pred indicating where it applies, with model variables vars and global parameters pars.
MassTransferValue[pred,vars,pars,lkey]
represents a mass transfer boundary condition with local parameters specified in pars[lkey].


MassTransferValue
MassTransferValue[pred,vars,pars]
represents a mass transfer boundary condition for PDEs with predicate pred indicating where it applies, with model variables vars and global parameters pars.
MassTransferValue[pred,vars,pars,lkey]
represents a mass transfer boundary condition with local parameters specified in pars[lkey].
Details


- MassTransferValue specifies a boundary condition for MassTransportPDEComponent and is used as part of the modeling equation:
- MassTransferValue is typically used to model the effect of a reactive flow outside the simulation domain.
- MassFluxValue models mass species transferred across some part of the boundary with dependent variable
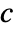 in [
in [![TemplateBox[{InterpretationBox[, 1], {"mol", , "/", , {"m", ^, 3}}, moles per meter cubed, {{(, "Moles", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"mol", , "/", , {"m", ^, 3}}, moles per meter cubed, {{(, "Moles", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/MassTransferValue.en/3.png) ], independent variables
], independent variables 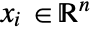 in [
in [![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/MassTransferValue.en/5.png) ] and time variable
] and time variable 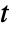 in [
in [![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/MassTransferValue.en/7.png) ].
]. - Stationary variables vars are vars={c[x1,…,xn],{x1,…,xn}}.
- Time-dependent variables vars are vars={c[t,x1,…,xn],t,{x1,…,xn}}.
- The non-conservative time-dependent mass transport model MassTransportPDEComponent is based on a convection-diffusion model with mass diffusivity
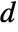 , mass convection velocity vector
, mass convection velocity vector 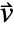 , mass reaction rate
, mass reaction rate 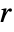 and mass source term
and mass source term 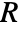 :
: - The conservative time-dependent mass transport model MassTransportPDEComponent is based on a conservative convection-diffusion model given by:
- The mass transfer value MassTransferValue with mass transfer coefficient
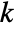 [
[![TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF]](Files/MassTransferValue.en/15.png) ], external mass concentration
], external mass concentration 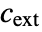 [
[![TemplateBox[{InterpretationBox[, 1], {"mol", , "/", , {"m", ^, 3}}, moles per meter cubed, {{(, "Moles", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"mol", , "/", , {"m", ^, 3}}, moles per meter cubed, {{(, "Moles", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/MassTransferValue.en/17.png) ] and boundary unit normal
] and boundary unit normal 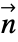 models:
models: - Model parameters pars as specified for MassTransportPDEComponent.
- The following additional model parameters pars can be given:
-
parameter default symbol "AmbientConcentration" - 0
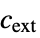 , external mass concentration [
, external mass concentration [![TemplateBox[{InterpretationBox[, 1], {"mol", , "/", , {"m", ^, 3}}, moles per meter cubed, {{(, "Moles", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"mol", , "/", , {"m", ^, 3}}, moles per meter cubed, {{(, "Moles", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/MassTransferValue.en/21.png) ]
]"MassTransferCoefficient" 1 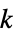 , mass transfer coefficient [
, mass transfer coefficient [![TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF]](Files/MassTransferValue.en/23.png) ]
] - All model parameters may depend on any of
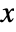 ,
, 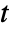 and
and 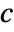 , as well as other dependent variables.
, as well as other dependent variables. - To localize model parameters, a key lkey can be specified, and values from association pars[lkey] are used for model parameters.
- MassTransferValue is a special case of a MassFluxValue.
- MassTransferValue evaluates to a generalized NeumannValue.
- The boundary predicate pred can be specified as in NeumannValue.
- If the MassTransferValue depends on parameters
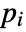 that are specified in the association pars as …,keypi…,pivi,…, the parameters
that are specified in the association pars as …,keypi…,pivi,…, the parameters 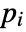 are replaced with
are replaced with 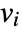 .
.
Examples
open all close allBasic Examples (2)
Scope (3)
Define model variables vars for a transient acoustic pressure field with model parameters pars and a specific boundary condition parameter:
Define model variables vars for a transient acoustic pressure field with model parameters pars and multiple specific parameter boundary conditions:
Model mass transport of a pollutant in a 2D rectangular region in an isotropic homogeneous medium. Initially, the pollutant concentration is zero throughout the region of interest. A concentration of 3000 ![]() is maintained at a strip with dimension 0.2
is maintained at a strip with dimension 0.2 ![]() located at the center of the left boundary, while the right boundary is subject to a parallel species flow with constant concentration of 1500
located at the center of the left boundary, while the right boundary is subject to a parallel species flow with constant concentration of 1500 ![]() , allowing for mass transfer. A pollutant outflow of 100
, allowing for mass transfer. A pollutant outflow of 100 ![]() is applied at both the top and bottom boundaries. A diffusion coefficient of 0.833
is applied at both the top and bottom boundaries. A diffusion coefficient of 0.833 ![]() is distributed uniformly with a uniform horizontal velocity of 0.01
is distributed uniformly with a uniform horizontal velocity of 0.01 ![]() :
:
Set up the mass transport model variables ![]() :
:
Set up a rectangular domain with a width of ![]() and a height of
and a height of ![]() :
:
Specify model parameters species diffusivity ![]() and fluid flow velocity
and fluid flow velocity ![]() :
:
Set up a species concentration source of 0.2 ![]() in length at the center of the left surface:
in length at the center of the left surface:
Set up a mass transfer boundary on the right surface:
Tech Notes
Related Guides
History
Text
Wolfram Research (2020), MassTransferValue, Wolfram Language function, https://reference.wolfram.com/language/ref/MassTransferValue.html.
CMS
Wolfram Language. 2020. "MassTransferValue." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MassTransferValue.html.
APA
Wolfram Language. (2020). MassTransferValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MassTransferValue.html
BibTeX
@misc{reference.wolfram_2025_masstransfervalue, author="Wolfram Research", title="{MassTransferValue}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/MassTransferValue.html}", note=[Accessed: 26-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_masstransfervalue, organization={Wolfram Research}, title={MassTransferValue}, year={2020}, url={https://reference.wolfram.com/language/ref/MassTransferValue.html}, note=[Accessed: 26-February-2026]}