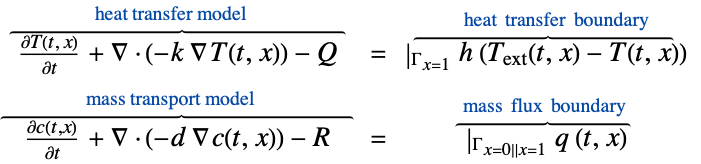MassFluxValue[pred,vars,pars]
represents a mass flux boundary condition for PDEs with predicate pred indicating where it applies, with model variables vars and global parameters pars.
MassFluxValue[pred,vars,pars,lkey]
represents a mass flux boundary condition with local parameters specified in pars[lkey].




MassFluxValue
MassFluxValue[pred,vars,pars]
represents a mass flux boundary condition for PDEs with predicate pred indicating where it applies, with model variables vars and global parameters pars.
MassFluxValue[pred,vars,pars,lkey]
represents a mass flux boundary condition with local parameters specified in pars[lkey].
Details



- MassFluxValue specifies a boundary condition for MassTransportPDEComponent and is used as part of the modeling equation:
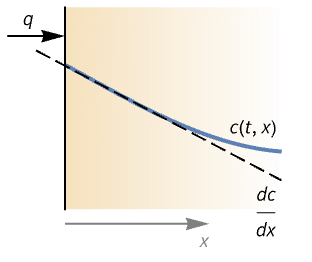
- MassFluxValue is typically used to model mass species flow through a boundary caused by a species source or sink outside of the domain.
- A flow rate is the flow of a quantity like energy or mass per time. Flux is the flow rate through the boundary and is measured in the units of the quantity per area per time. A millimeter of rain per cross section of opening area per hour is a rain flux.
- MassFluxValue models the rate of mass species flowing through some part of the boundary with dependent variable
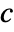 in [
in [![TemplateBox[{InterpretationBox[, 1], {"mol", , "/", , {"m", ^, 3}}, moles per meter cubed, {{(, "Moles", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"mol", , "/", , {"m", ^, 3}}, moles per meter cubed, {{(, "Moles", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/MassFluxValue.en/4.png) ], independent variables
], independent variables 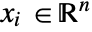 in [
in [![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/MassFluxValue.en/6.png) ] and time variable
] and time variable 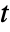 in [
in [![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/MassFluxValue.en/8.png) ].
]. - Stationary variables vars are vars={c[x1,…,xn],{x1,…,xn}}.
- Time-dependent variables vars are vars={c[t,x1,…,xn],t,{x1,…,xn}}.
- The non-conservative time-dependent mass transport model MassTransportPDEComponent is based on a convection-diffusion model with mass diffusivity
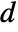 , mass convection velocity vector
, mass convection velocity vector 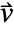 , mass reaction rate
, mass reaction rate 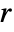 and mass source term
and mass source term 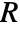 :
: - The conservative time-dependent mass transport model MassTransportPDEComponent is based on a conservative convection-diffusion model given by:
- In the non-conservative form, MassFluxValue with mass flux
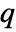 in
in 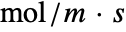 and boundary unit normal
and boundary unit normal 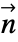 models:
models: - In the conservative form, MassFluxValue models:
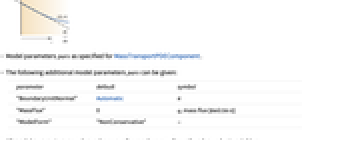
- Model parameters pars as specified for MassTransportPDEComponent.
- The following additional model parameters pars can be given:
-
parameter default symbol "BoundaryUnitNormal" Automatic 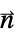
"MassFlux" - 0
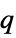 , mass flux [
, mass flux [![TemplateBox[{InterpretationBox[, 1], {"mol", , "/(", , "m", , "s", , ")"}, moles per meter second, {{(, "Moles", )}, /, {(, {"Meters", , "Seconds"}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"mol", , "/(", , "m", , "s", , ")"}, moles per meter second, {{(, "Moles", )}, /, {(, {"Meters", , "Seconds"}, )}}}, QuantityTF]](Files/MassFluxValue.en/23.png) ]
]"ModelForm" "NonConservative" - - All model parameters may depend on any of
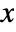 ,
, 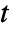 and
and 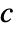 , as well as other dependent variables.
, as well as other dependent variables. - To localize model parameters, a key lkey can be specified, and values from association pars[lkey] are used for model parameters.
- MassFluxValue evaluates to a NeumannValue.
- The boundary predicate pred can be specified as in NeumannValue.
- If the MassFluxValue depends on parameters
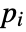 that are specified in the association pars as …,keypi…,pivi,…, the parameters
that are specified in the association pars as …,keypi…,pivi,…, the parameters 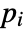 are replaced with
are replaced with 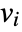 .
.

Examples
open all close allBasic Examples (2)
Scope (10)
Basic Examples (2)
1D (1)
Model a 1D chemical species field in an incompressible fluid whose right side and left side are subjected to a mass concentration and inflow condition, respectively:
Set up the stationary mass transport model variables ![]() :
:
Specify the mass transport model parameters species diffusivity ![]() and fluid flow velocity
and fluid flow velocity ![]() :
:
Specify a species flux boundary condition:
2D (1)
Model mass transport of a pollutant in a 2D rectangular region in an isotropic homogeneous medium. Initially, the pollutant concentration is zero throughout the region of interest. A concentration of 3000 ![]() is maintained at a strip with dimension 0.2
is maintained at a strip with dimension 0.2 ![]() located at the center of the left boundary, while the right boundary is subject to a parallel species flow with a constant concentration of 1500
located at the center of the left boundary, while the right boundary is subject to a parallel species flow with a constant concentration of 1500 ![]() , allowing for mass transfer. A pollutant outflow of 100
, allowing for mass transfer. A pollutant outflow of 100 ![]() is applied at both the top and bottom boundaries. A diffusion coefficient of 0.833
is applied at both the top and bottom boundaries. A diffusion coefficient of 0.833 ![]() is distributed uniformly with a uniform horizontal velocity of 0.01
is distributed uniformly with a uniform horizontal velocity of 0.01 ![]() :
:
Set up the mass transport model variables ![]() :
:
Set up a rectangular domain with a width of ![]() and a height of
and a height of ![]() :
:
Specify model parameters species diffusivity ![]() and fluid flow velocity
and fluid flow velocity ![]() :
:
Set up a species concentration source of 0.2 ![]() length at the center of the left surface:
length at the center of the left surface:
Set up a mass transfer boundary on the right surface:
3D (1)
Model a non-conservative chemical species field in a unit cubic domain, with two mass conditions at two lateral surfaces and a mass inflow through a circle with radius 0.2 ![]() at the center of the top surface, as well as an orthotropic mass diffusivity
at the center of the top surface, as well as an orthotropic mass diffusivity ![]() :
:
Set up the mass transport model variables ![]() :
:
Specify a diffusivity ![]() and a flow velocity field
and a flow velocity field ![]() :
:
Specify a flux condition ![]() of
of ![]() through a regional circle on the top surface:
through a regional circle on the top surface:
Material Regions (1)
Model a 1D chemical species transport through different material with a reaction rate in one. The right side and left side are subjected to a mass concentration and inflow condition, respectively:
Set up the stationary mass transport model variables ![]() :
:
Specify the mass transport model parameters species diffusivity ![]() and a reaction rate
and a reaction rate ![]() active in the region
active in the region ![]() :
:
Specify a species flux boundary condition:
Time Dependent (1)
Model a 1D non-conservative chemical species field and a mass flux through part of the boundary with:
Set up the time-dependent mass transport model variables ![]() :
:
Specify the mass transport model parameters mass diffusivity ![]() and mass convection velocity
and mass convection velocity ![]() :
:
Set up the equation with a mass flux ![]() of
of ![]() at the left end for the first 50 seconds:
at the left end for the first 50 seconds:
Solve the PDE with an initial condition of a zero concentration:
Nonlinear Time Dependent (1)
Model a 1D non-conservative chemical species field with a nonlinear diffusivity coefficient ![]() and an outflow condition through part of the boundary, which is expressed as follows:
and an outflow condition through part of the boundary, which is expressed as follows:
Set up the mass transport model variables ![]() :
:
Specify a nonlinear species diffusivity ![]() and fluid flow velocity
and fluid flow velocity ![]() :
:
Specify an outflow flux ![]() of
of ![]() applied at the right end:
applied at the right end:
Specify a time-dependent mass concentration surface condition:
Coupled Time Dependent (2)
Model a 1D coupled non-conservative dual chemical species field with corresponding mass flux through the left parts of the boundary:
Set up the time dependent mass transport model variables ![]() for the
for the ![]() and
and ![]() species, respectively:
species, respectively:
Specify the mass transport model parameters mass diffusivity ![]() and
and ![]() for the
for the ![]() and
and ![]() species:
species:
Set up the boundary conditions with a mass flux ![]() of
of ![]() and
and ![]() for
for ![]() and
and ![]() at the left end for the first 50 seconds:
at the left end for the first 50 seconds:
Model a 1D coupled chemical species field with a convection velocity and a mass flux through the left boundary:
Set up the time-dependent mass transport model variables ![]() for
for ![]() and
and ![]() species, respectively:
species, respectively:
Specify the mass transport model parameters mass diffusivity ![]() and
and ![]() for the
for the ![]() and
and ![]() species:
species:
Set up the equation with a mass flux ![]() of 6
of 6 ![]() and 12
and 12 ![]() for
for ![]() and
and ![]() at the left end for the first 50 seconds:
at the left end for the first 50 seconds:
Applications (2)
Single Equation (1)
Model mass transport of a pollutant in a 2D rectangular region in an isotropic homogeneous medium. Initially, the pollutant concentration is zero throughout the region of interest. A concentration of 3000 ![]() is maintained at a strip with dimension 0.2
is maintained at a strip with dimension 0.2 ![]() located at the center of the left boundary, while a pollutant outflow of 100
located at the center of the left boundary, while a pollutant outflow of 100 ![]() is applied at both the top and bottom boundaries. A diffusion coefficient of 0.833
is applied at both the top and bottom boundaries. A diffusion coefficient of 0.833 ![]() is distributed uniformly, but both horizontal and vertical velocity are spatial dependent:
is distributed uniformly, but both horizontal and vertical velocity are spatial dependent:
Set up the mass transport model variables ![]() :
:
Set up a rectangular domain with a width of ![]() and a height of
and a height of ![]() :
:
Specify model parameters species diffusivity ![]() and fluid flow velocity
and fluid flow velocity ![]() :
:
Set up a species concentration source of 0.2 ![]() length at the center of the left surface:
length at the center of the left surface:
Coupled Equations (1)
Solve a coupled heat transfer and mass transport model with a thermal transfer value and a mass flux value on the boundary:
Set up the heat transfer mass transport model variables ![]() :
:
Specify heat transfer and mass transport model parameters, heat source ![]() , thermal conductivity
, thermal conductivity ![]() , mass diffusivity
, mass diffusivity ![]() and mass source
and mass source ![]() :
:
Specify boundary condition parameters for a thermal convection value with an external flow temperature ![]() of 1000 K and a heat transfer coefficient
of 1000 K and a heat transfer coefficient ![]() of
of ![]() :
:
Tech Notes
Related Guides
History
Text
Wolfram Research (2020), MassFluxValue, Wolfram Language function, https://reference.wolfram.com/language/ref/MassFluxValue.html.
CMS
Wolfram Language. 2020. "MassFluxValue." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MassFluxValue.html.
APA
Wolfram Language. (2020). MassFluxValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MassFluxValue.html
BibTeX
@misc{reference.wolfram_2025_massfluxvalue, author="Wolfram Research", title="{MassFluxValue}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/MassFluxValue.html}", note=[Accessed: 09-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_massfluxvalue, organization={Wolfram Research}, title={MassFluxValue}, year={2020}, url={https://reference.wolfram.com/language/ref/MassFluxValue.html}, note=[Accessed: 09-January-2026]}