MassSymmetryValue[pred,vars,pars]
represents a mass symmetry boundary condition for PDEs with predicate pred indicating where it applies, with model variables vars and global parameters pars.
MassSymmetryValue[pred,vars,pars,lkey]
represents a mass symmetry boundary condition with local parameters specified in pars[lkey].


MassSymmetryValue
MassSymmetryValue[pred,vars,pars]
represents a mass symmetry boundary condition for PDEs with predicate pred indicating where it applies, with model variables vars and global parameters pars.
MassSymmetryValue[pred,vars,pars,lkey]
represents a mass symmetry boundary condition with local parameters specified in pars[lkey].
Details


- MassSymmetryValue specifies a boundary condition for MassTransportPDEComponent and is used as part of the modeling equation:
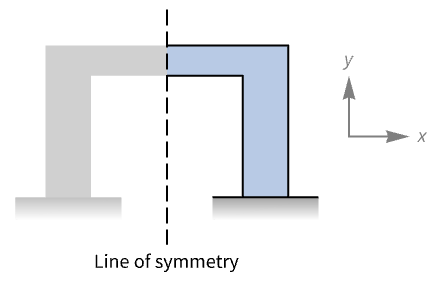
- MassSymmetryValue is typically used to model a boundary with mirror symmetry along an axis.
- MassSymmetryValue models a boundary with mirror symmetry with dependent variable
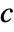 in [
in [![TemplateBox[{InterpretationBox[, 1], {"mol", , "/", , {"m", ^, 3}}, moles per meter cubed, {{(, "Moles", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"mol", , "/", , {"m", ^, 3}}, moles per meter cubed, {{(, "Moles", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/MassSymmetryValue.en/4.png) ], independent variables
], independent variables 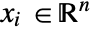 in [
in [![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/MassSymmetryValue.en/6.png) ] and time variable
] and time variable 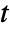 in [
in [![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/MassSymmetryValue.en/8.png) ].
]. - Stationary variables vars are vars={c[x1,…,xn],{x1,…,xn}}.
- Time-dependent variables vars are vars={c[t,x1,…,xn],t,{x1,…,xn}}.
- The non-conservative-time dependent mass transport model MassTransportPDEComponent is based on a convection-diffusion model with mass diffusivity
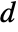 , mass convection velocity vector
, mass convection velocity vector 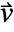 , mass reaction rate
, mass reaction rate 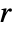 and mass source term
and mass source term 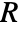 :
: - The conservative time-dependent mass transport model MassTransportPDEComponent is based on a conservative convection-diffusion model given by:
- The normal flow velocity
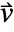 on the symmetry boundary will remain at zero at all times.
on the symmetry boundary will remain at zero at all times. - Both in the conservative and non-conservative forms, MassSymmetryValue with boundary unit normal
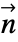 models:
models: - Model parameters pars as specified for MassTransportPDEComponent.
- The following additional model parameters pars can be given:
-
parameter default symbol "ModelForm" "NonConservative" 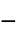
- MassSymmetryValue is effectively the same as MassFluxValue with a heat flux of 0.
- The boundary predicate pred can be specified as in NeumannValue.
- If the MassSymmetryValue depends on parameters
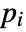 that are specified in the association pars as …,keypi…,pivi,…, the parameters
that are specified in the association pars as …,keypi…,pivi,…, the parameters 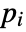 are replaced with
are replaced with 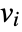 .
.
Examples
open all close allBasic Examples (3)
Set up a mass symmetry boundary condition:
Set up a system of mass symmetry boundary conditions:
Symmetry boundaries can be used to reduce the size of the geometry of the model. Set up a mass transport equation:
Set up and visualize a region:
Solve and visualize the equation:
Set up a region about the symmetry axis at ![]() :
:
Solve and visualize the equation with a symmetry boundary at ![]() :
:
Tech Notes
Related Guides
History
Text
Wolfram Research (2020), MassSymmetryValue, Wolfram Language function, https://reference.wolfram.com/language/ref/MassSymmetryValue.html.
CMS
Wolfram Language. 2020. "MassSymmetryValue." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MassSymmetryValue.html.
APA
Wolfram Language. (2020). MassSymmetryValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MassSymmetryValue.html
BibTeX
@misc{reference.wolfram_2025_masssymmetryvalue, author="Wolfram Research", title="{MassSymmetryValue}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/MassSymmetryValue.html}", note=[Accessed: 05-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_masssymmetryvalue, organization={Wolfram Research}, title={MassSymmetryValue}, year={2020}, url={https://reference.wolfram.com/language/ref/MassSymmetryValue.html}, note=[Accessed: 05-January-2026]}