

MeanShift
Details and Options


- MeanShift is also known as mode seeking and is typically used to smooth data arrays and images.
- MeanShift preserves the ordering of the input elements.
- In MeanShift[image,d,parts], parts can be a marker image or a list of {row,column} positions.
- The following options can be given:
-
DistanceFunction EuclideanDistance distance metric function MaxIterations 1 maximum number of iterations to perform Tolerance 0 allowed tolerance to assume convergence Weights Automatic weights to use for computing the mean - With Tolerance->t, mean-shift iterations stop if no point changes by more than t.
- By default, unit weights are used. Using Weights->f, function f applied to rescaled distances between elements is used to compute and return a weighted mean of the values. Distances between 0 and d are rescaled to be in the range from 0 and 1.
- Typical settings for Weights include:
-
UnitStep unit weights (default) UnitTriangle linearly decreasing weight "Gaussian" weights based on a Gaussian window with sigma 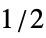
{"Gaussian",σ} Gaussian window with sigma σ - Common settings for the DistanceFunction option are:
-
ManhattanDistance Manhattan or "city block" distance EuclideanDistance Euclidean distance SquaredEuclideanDistance squared Euclidean distance NormalizedSquaredEuclideanDistance normalized squared Euclidean distance CosineDistance angular cosine distance CorrelationDistance correlation coefficient distance f use an arbitrary function f
Examples
open all close allBasic Examples (3)
Scope (4)
Options (8)
DistanceFunction (3)
By default, EuclideanDistance is used:
MaxIterations (2)
By default, only one iteration of mean shift is applied to input:
Use MaxIterations to specify the number of iterations:
Use MaxIterations->Infinity to run until convergence:
Use MaxIterations to iteratively smooth data:
Applications (9)
Smoothing (2)
Find large-scale features in a noisy dataset:
Image smoothing using mean shift of 5D features in the joint spatial-range domain:
Use LABColor values, suitable for computing color distances:
Compute spatial location features normalized to the range 0 to 1:
Construct 5D features from color and location of pixels:
Perform one iteration of mean-shift filtering using "Gaussian" weights and EuclideanDistance, which is equivalent to multiplying Gaussian-weighted spatial and range features:
Mean-Shift Displacement (2)
Find Modes of Estimated Distribution (1)
Clustering (2)
Generate data from some distribution:
Apply mean shift until all data points have converged:
Gather the result into clusters:
Generate a large amount of data from some distribution:
Compute trajectories for a fraction of the data samples:
Merge paths that end within radius of each other:
Label each trajectory and compute the corresponding nearest function:
Each unlabeled sample is assigned the label of the closest trajectory:
Computing the mean shift until convergence for the entire dataset would take much longer:
Properties & Relations (3)
Perform mean shift on some parts of a list:
Extract the mean-shifted elements:
Perform mean shift on some parts of an image:
Create a mask for the first detected bright component:
Extract the mean-shifted pixel values:
The mean-shift vector is proportional to the gradient density estimate normalized by the density estimate:
See Also
Related Guides
Text
Wolfram Research (2010), MeanShift, Wolfram Language function, https://reference.wolfram.com/language/ref/MeanShift.html (updated 2014).
CMS
Wolfram Language. 2010. "MeanShift." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/MeanShift.html.
APA
Wolfram Language. (2010). MeanShift. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MeanShift.html
BibTeX
@misc{reference.wolfram_2025_meanshift, author="Wolfram Research", title="{MeanShift}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/MeanShift.html}", note=[Accessed: 25-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_meanshift, organization={Wolfram Research}, title={MeanShift}, year={2014}, url={https://reference.wolfram.com/language/ref/MeanShift.html}, note=[Accessed: 25-January-2026]}