MeijerG
✖
MeijerG
例題
すべて開くすべて閉じる例 (6)基本的な使用例
https://wolfram.com/xid/0ftsl9u-hd0tyg
多くの特殊関数はMeijerGの特殊形である:
https://wolfram.com/xid/0ftsl9u-syxz3e
https://wolfram.com/xid/0ftsl9u-exgo4e
https://wolfram.com/xid/0ftsl9u-m51
https://wolfram.com/xid/0ftsl9u-b5yjf1
https://wolfram.com/xid/0ftsl9u-f65ufv
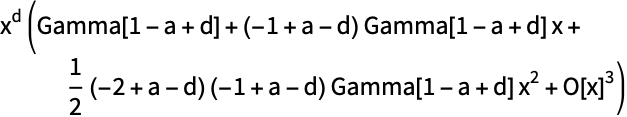
Infinityにおける級数展開:
https://wolfram.com/xid/0ftsl9u-fgrnr3
スコープ (35)標準的な使用例のスコープの概要
数値評価 (7)
https://wolfram.com/xid/0ftsl9u-l274ju
https://wolfram.com/xid/0ftsl9u-cksbl4
https://wolfram.com/xid/0ftsl9u-b0wt9
https://wolfram.com/xid/0ftsl9u-y7k4a
https://wolfram.com/xid/0ftsl9u-hfml09
https://wolfram.com/xid/0ftsl9u-di5gcr

https://wolfram.com/xid/0ftsl9u-bq2c6r
MeijerGは第3引数のリストに要素単位で縫い込まれる:
https://wolfram.com/xid/0ftsl9u-bhng5j
MeijerGは第3引数の疎な配列と構造化配列に要素単位で縫い込まれる:
https://wolfram.com/xid/0ftsl9u-izuq9r

https://wolfram.com/xid/0ftsl9u-bvrzed
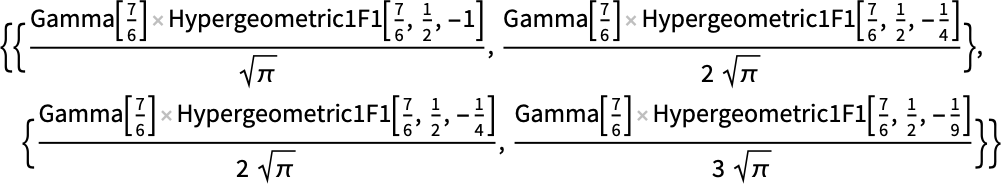
Aroundを使って平均的な場合の統計区間を計算する:
https://wolfram.com/xid/0ftsl9u-cw18bq
https://wolfram.com/xid/0ftsl9u-thgd2
MatrixFunctionを使って行列のMeijerG関数を計算することもできる:
https://wolfram.com/xid/0ftsl9u-o5jpo
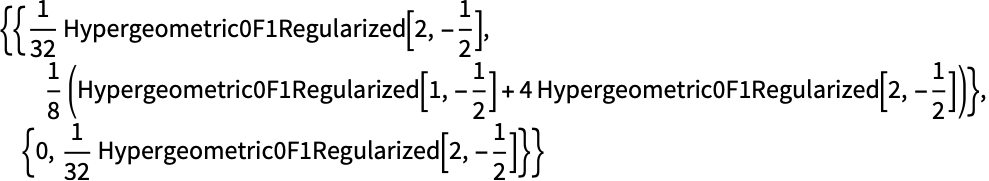
特定の値 (5)
https://wolfram.com/xid/0ftsl9u-o7spmt
https://wolfram.com/xid/0ftsl9u-bjvvy9
https://wolfram.com/xid/0ftsl9u-jql9vr
https://wolfram.com/xid/0ftsl9u-h2sg3
https://wolfram.com/xid/0ftsl9u-jevg27
https://wolfram.com/xid/0ftsl9u-bqgyg7
https://wolfram.com/xid/0ftsl9u-6ak4h
単純なパラメータについてMeijerGを評価するとより単純な関数になる:
https://wolfram.com/xid/0ftsl9u-ih9u38
https://wolfram.com/xid/0ftsl9u-batwwb
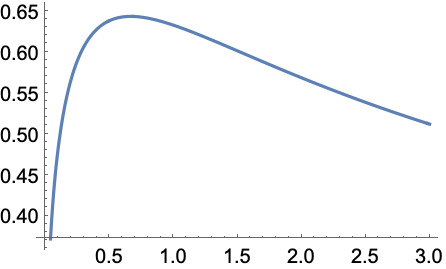
MeijerG[{{},{}},{{1/2},{3/2}},x]の正の最小値を求める:
https://wolfram.com/xid/0ftsl9u-f2hrld
https://wolfram.com/xid/0ftsl9u-hcwjf6
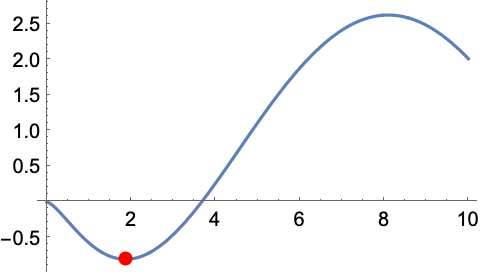
可視化 (2)
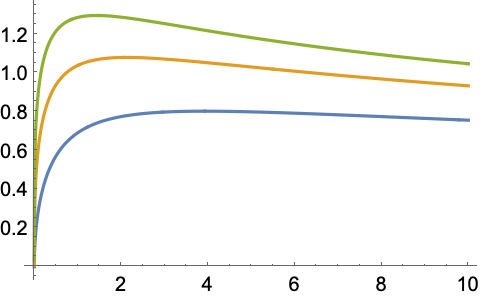
MeijerG関数をさまざまなパラメータについてプロットする:
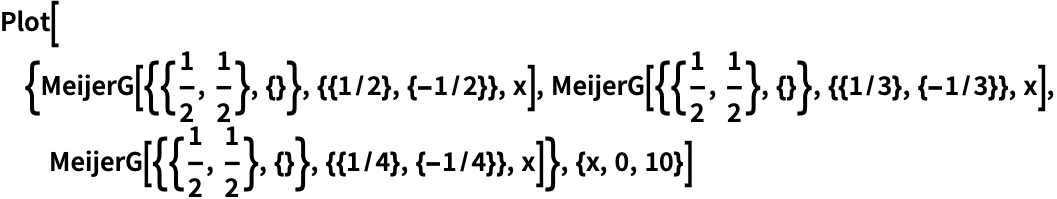
https://wolfram.com/xid/0ftsl9u-c0x9p4
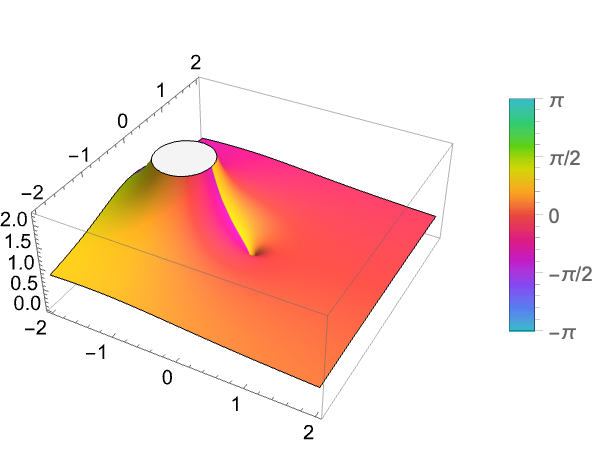
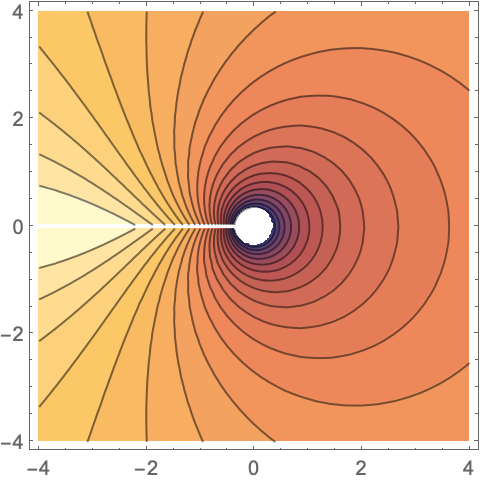
MeijerG[{{1},{}},{{1/2,1,3/2},{}},z ]の実部をプロットする:
https://wolfram.com/xid/0ftsl9u-kgd8nu
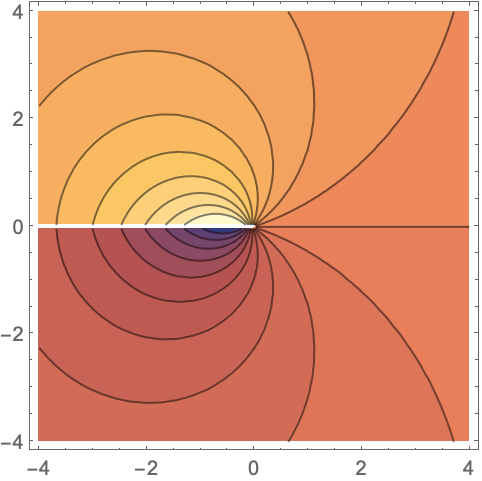
MeijerG[{{1},{}},{{1/2,1,3/2},{}},z ]の虚部をプロットする:
https://wolfram.com/xid/0ftsl9u-oqui6b
関数の特性 (9)
https://wolfram.com/xid/0ftsl9u-w67qyz
https://wolfram.com/xid/0ftsl9u-gkyjuv
MeijerGは要素単位でリストと最後の引数に縫い込まれる:
https://wolfram.com/xid/0ftsl9u-muz25u
https://wolfram.com/xid/0ftsl9u-h5x4l2
https://wolfram.com/xid/0ftsl9u-mdtl3h
https://wolfram.com/xid/0ftsl9u-mn5jws
https://wolfram.com/xid/0ftsl9u-nlz7s
https://wolfram.com/xid/0ftsl9u-poz8g
https://wolfram.com/xid/0ftsl9u-ctca0g
https://wolfram.com/xid/0ftsl9u-cxk3a6
https://wolfram.com/xid/0ftsl9u-frlnsr
https://wolfram.com/xid/0ftsl9u-84dui
https://wolfram.com/xid/0ftsl9u-8kku21
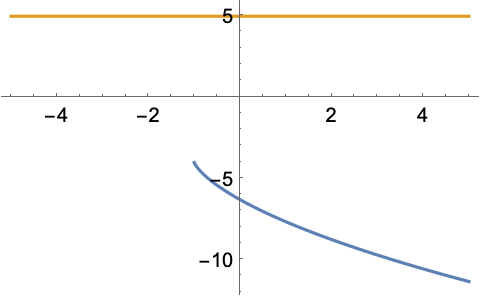
TraditionalFormによる表示:
https://wolfram.com/xid/0ftsl9u-d5dvhu
https://wolfram.com/xid/0ftsl9u-kwtb0
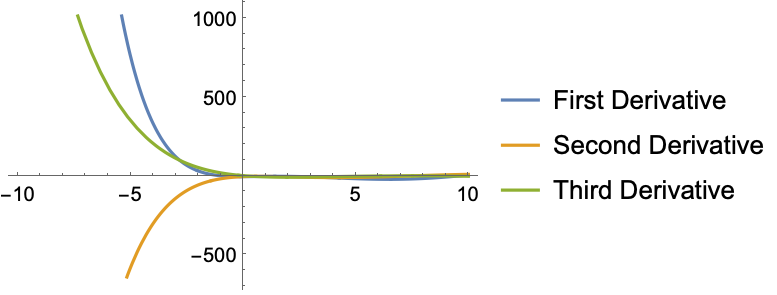
微分 (3)
積分 (3)
Integrateを使って不定積分を計算する:
https://wolfram.com/xid/0ftsl9u-bponid
https://wolfram.com/xid/0ftsl9u-op9yly
https://wolfram.com/xid/0ftsl9u-bfdh5d
https://wolfram.com/xid/0ftsl9u-4nbst
https://wolfram.com/xid/0ftsl9u-yncg8
級数展開 (6)
Seriesを使ってテイラー(Taylor)展開を求める:
https://wolfram.com/xid/0ftsl9u-ewr1h8
https://wolfram.com/xid/0ftsl9u-binhar
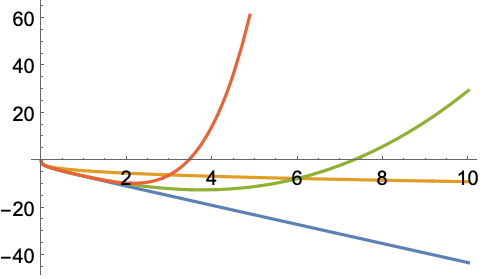
SeriesCoefficientを使った級数展開における一般項:
https://wolfram.com/xid/0ftsl9u-dznx2j
Infinityにおける級数展開を求める:
https://wolfram.com/xid/0ftsl9u-syq
https://wolfram.com/xid/0ftsl9u-0egdf
https://wolfram.com/xid/0ftsl9u-jwxla7
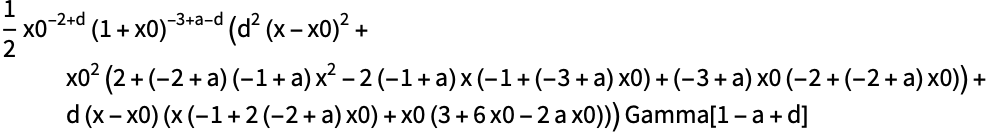
一般化と拡張 (1)一般化および拡張された使用例
アプリケーション (5)この関数で解くことのできる問題の例
BetaDistributionから導かれた独立確率変数の積を定義する:

https://wolfram.com/xid/0ftsl9u-hitydv

https://wolfram.com/xid/0ftsl9u-hmvu4v
FunctionExpandを使い,より単純な関数によってこれを表現する:
https://wolfram.com/xid/0ftsl9u-ky14tp
PDFのプロットをランダムなサンプルのHistogramと比較する:
https://wolfram.com/xid/0ftsl9u-ehgwjq
https://wolfram.com/xid/0ftsl9u-ott6k
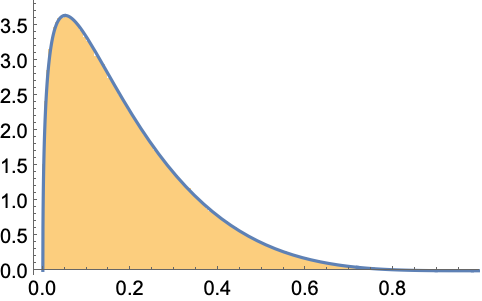
https://wolfram.com/xid/0ftsl9u-g34byp
MeijerGは対数部分を返す:
https://wolfram.com/xid/0ftsl9u-j7c1s1

IntegrateはMeijerGを含む答を返すことがある:
https://wolfram.com/xid/0ftsl9u-79bruc
https://wolfram.com/xid/0ftsl9u-eu5lw7
三次特異常微分方程式をHypergeometricPFQ関数とMeijerG関数で解く:
https://wolfram.com/xid/0ftsl9u-jvopp

https://wolfram.com/xid/0ftsl9u-e5ez2u
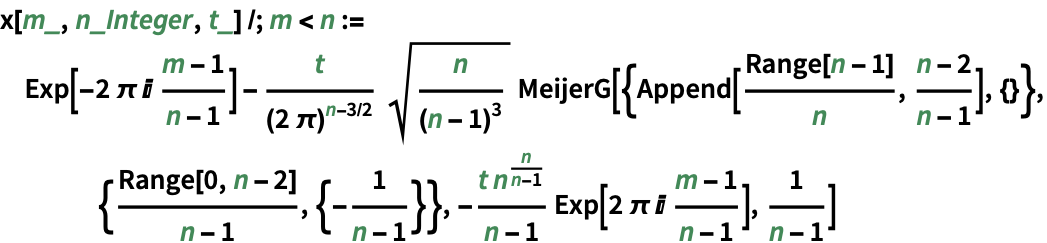
https://wolfram.com/xid/0ftsl9u-d8ja4
https://wolfram.com/xid/0ftsl9u-kvcatk
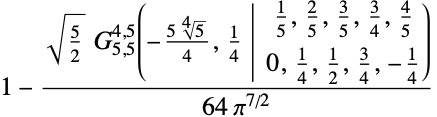
https://wolfram.com/xid/0ftsl9u-isknwz
https://wolfram.com/xid/0ftsl9u-5wjl0
特性と関係 (1)この関数の特性および他の関数との関係
FunctionExpandを使ってMeijerGをより簡単な関数に展開する:
https://wolfram.com/xid/0ftsl9u-2pfvc
https://wolfram.com/xid/0ftsl9u-csyjt5
考えられる問題 (3)よく起る問題と予期しない動作
パラメータによっては,MeijerGが定義されないことがある:
https://wolfram.com/xid/0ftsl9u-tx106
![]() は
は ![]() のときのMeijerG関数の特異点である:
のときのMeijerG関数の特異点である:
https://wolfram.com/xid/0ftsl9u-goaj2u
https://wolfram.com/xid/0ftsl9u-e6gldl
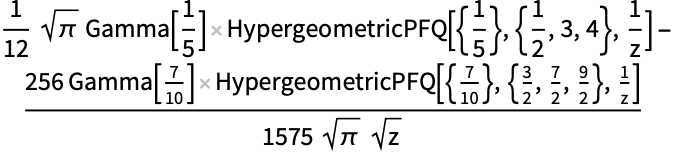
https://wolfram.com/xid/0ftsl9u-c79hns
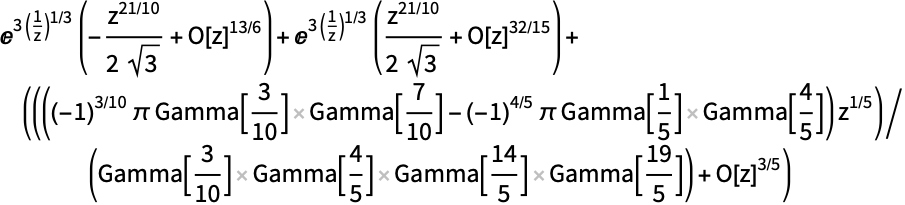
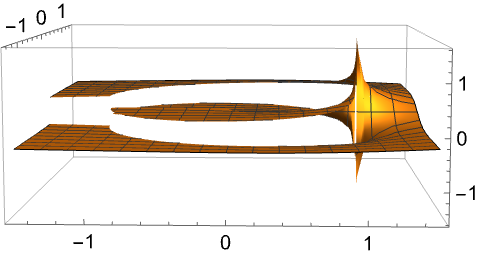
![]() のとき,MeijerGは区分分析関数である:
のとき,MeijerGは区分分析関数である:
https://wolfram.com/xid/0ftsl9u-dtuz8f
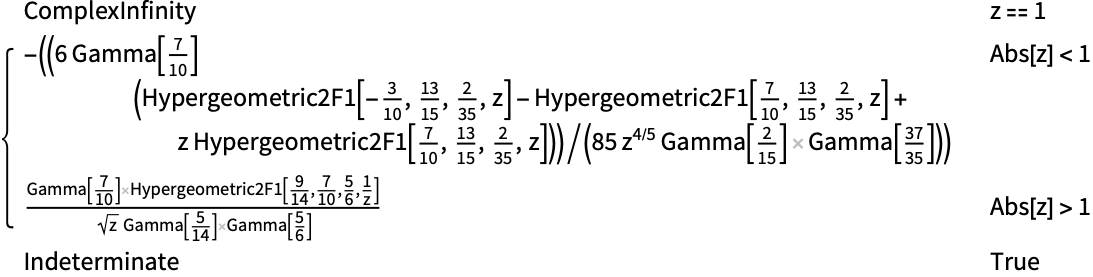
https://wolfram.com/xid/0ftsl9u-gq3uxz
おもしろい例題 (2)驚くような使用例や興味深い使用例
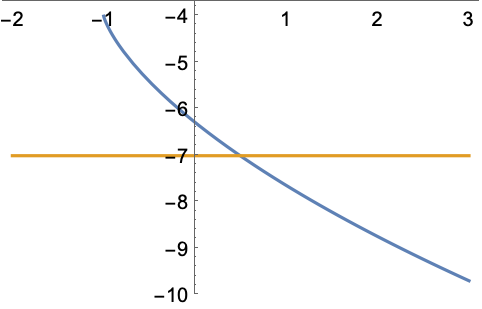
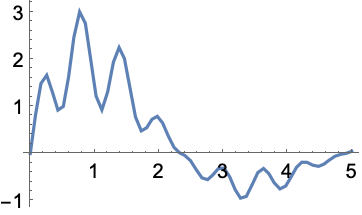
SIAM 100‐digitチャレンジ問題を解く.最大化するために ![]() を求める:
を求める:
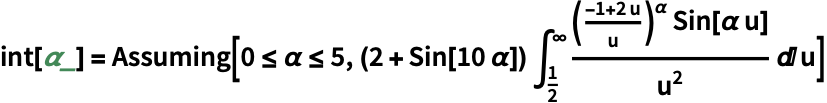
https://wolfram.com/xid/0ftsl9u-ghzx25
https://wolfram.com/xid/0ftsl9u-lfb7tc

https://wolfram.com/xid/0ftsl9u-k67mu
MeijerGの特殊形として多くの初等関数および特殊関数を生成する:
https://wolfram.com/xid/0ftsl9u-fclgt
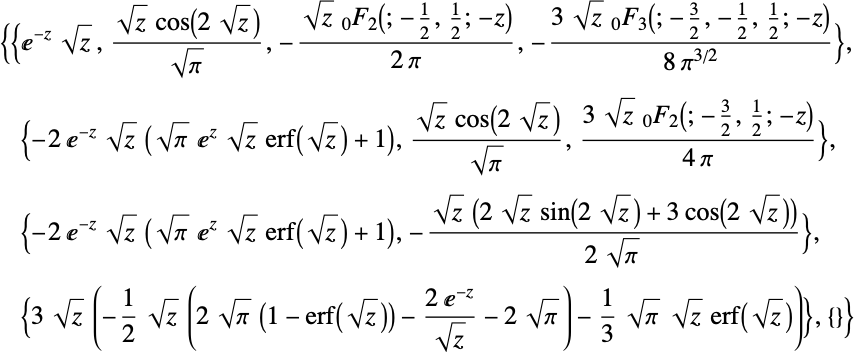
Wolfram Research (1996), MeijerG, Wolfram言語関数, https://reference.wolfram.com/language/ref/MeijerG.html.テキスト
Wolfram Research (1996), MeijerG, Wolfram言語関数, https://reference.wolfram.com/language/ref/MeijerG.html.
Wolfram Research (1996), MeijerG, Wolfram言語関数, https://reference.wolfram.com/language/ref/MeijerG.html.CMS
Wolfram Language. 1996. "MeijerG." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MeijerG.html.
Wolfram Language. 1996. "MeijerG." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MeijerG.html.APA
Wolfram Language. (1996). MeijerG. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MeijerG.html
Wolfram Language. (1996). MeijerG. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MeijerG.htmlBibTeX
@misc{reference.wolfram_2025_meijerg, author="Wolfram Research", title="{MeijerG}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/MeijerG.html}", note=[Accessed: 04-April-2025
]}BibLaTeX
@online{reference.wolfram_2025_meijerg, organization={Wolfram Research}, title={MeijerG}, year={1996}, url={https://reference.wolfram.com/language/ref/MeijerG.html}, note=[Accessed: 04-April-2025
]}