MengerMesh
MengerMesh[n]
给出表示第 n![]() 步门格海绵的网格区域.
步门格海绵的网格区域.
MengerMesh[n,d]
给出 d 维门格海绵的第 n![]() 步.
步.
更多信息和选项

- MengerMesh 亦称为谢尔宾斯基地毯.
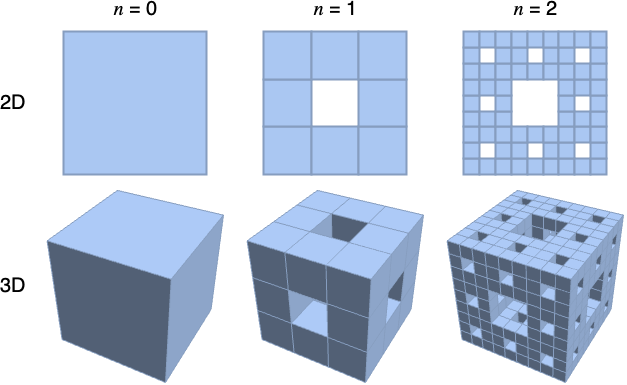
- MengerMesh[n] 通过重复移除单位正方形及后续单元中间的小正方形而产生. »
- MengerMesh[n] 等价于 MengerMesh[n,2].
- MengerMesh 接受和 MeshRegion 一样的选项,额外选项如下所示:
-
DataRange Automatic 生成的网格坐标的范围
范例
打开所有单元关闭所有单元选项 (12)
DataRange (1)
DataRange 允许指定所生成的网格坐标的范围:
MeshCellHighlight (2)
MeshCellLabel (2)
MeshCellMarker (1)
MeshCellMarker 可用来为部分 MengerMesh 赋值:
用 MeshCellLabel 显示标记:
MeshCellShapeFunction (2)
MeshCellStyle (2)
属性和关系 (7)
MengerMesh 总是输出 MeshRegion 的全部:
二维情况下,MengerMesh 由正方形组成:
三维 MengerMesh(门格海绵) 的每个面都是一个二维 MengerMesh(谢尔宾斯基地毯) :
求 MengerMesh 的边界网格区域:
DataRange->range 等价于使用 RescalingTransform[{...},range]:
可能存在的问题 (1)
MengerMesh 有可能太大,无法生成:
Wolfram Research (2017),MengerMesh,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MengerMesh.html.
文本
Wolfram Research (2017),MengerMesh,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MengerMesh.html.
CMS
Wolfram 语言. 2017. "MengerMesh." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/MengerMesh.html.
APA
Wolfram 语言. (2017). MengerMesh. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MengerMesh.html 年